شروڈنگر مساوات

کوانٹم مکینکس وچ, شروڈنگر اکیوئیشن اک اجیہی ریاضیاتی مساوات ہندی اے جو کسے اجیاے بھوتکی سسٹم دیاں وقت بیتن مگروں تبدیلیاں نوں درساؤندی اے, جہناں وچ کوانٹم اثر, جویں ویو-پارٹیکل ڈیولٹی, اہم ہو جاندے ہن۔ ایہہ اکیوئیشن کوانٹم مکینیکل سسٹماں دا مطالعہ کرن لئی اک گنتک فارمولا ویونتبندی اے۔ ایہہ کوانٹم سسٹماں دے مطالعہ لئی اک مرکزی نتیجہ منی جاندی اے اتے اسدی ویونتبندی کوانٹم مکینکس دی تھیوری ترقی یافتہ کرن وچ اک اہم میلپتھر رہی سی۔ اسدا نام ایرون شروڈنگر دے نام توں رکھیا گیا سی, جسنے 1925 وچ مساوات ویونتبند کیتی سی اتے 1933 وچ فزکس وچ نوبل انعام جتن دا نتیجہ دین والے اسدے کم دا ادھار رچدے ہوئے 1926 وچ چھاپی سی۔^[۱]^[۲] ایہہ اکیوئیشن کسے ویو مساوات دے طور تے جانی جاندی اک قسم دی ڈفرینشیئل اکیوئیشن اے, جو ترنگاں دی ہلجلّ دے اک گنتک ماڈل دے طور تے کم کردی اے۔

کلاسیکل مکینکس اندر, نیوٹن دا دوجا قنون ( $F = m a$ ) کوئی گنتک اندازا لگاؤن لئی ورتیا جاندا اے کہ معلوم شروع شرطاں دا کوئی سیٹ اپناؤناں ہویا کوئی دتا ہویا سسٹم کہڑا رستہ اپنائیگا۔ کوانٹم مکینکس اندر, کسے کوانٹم سسٹم (عامطور تے ایٹم, مولیکولر, اتے سبئیٹومک کن, چااے آزاد ہون, چااے بنے ہوئے جاں ستھانبدھّ کیتے ہوئے ہون) واسطے شروڈنگر اکیوئیشن , نیوٹن دے نیم دا تلّ (اینالوگ) ہندی اے۔ ایہہ کوئی آسان الجبرک اکیوئیشن نہیں ہندی, سگوں عامطور تے اک ریکھک انشک ڈفرینشیئل مساوات ہندی اے, جو سسٹم دے ویو فنکشن (جسنوں حالت فنکشن وی کیہا جاندا اے) دی سماں-اتپتی نوں درسا رہی ہندی اے۔^[۳]^:1–2

ویو فنکشن دی دھارنا اک بنیادی کوانٹم مکینکس دا سوے-سدھ اصول اے۔ ایہناں سوے-سدھ نظریات دی ورتوں نال, شروڈنگر اکیوئیشن نوں اس حقیقت توں ویونتبند کیتا جا سکدا اے کہ سماں-اتپتی اوپریٹر ضرور ہی یونائٹری ہونے چاہیدے ہن اتے لازمی طور تے اسے کرکے کسے سوے-اڈجوآئنٹ اوپریٹر دے ایکپونینشیئل ولوں پیدا ہونے چاہیدے ہن, جو کوانٹم ہیملٹونیئن ہندا اے۔ ویونتبندی نوں ہیٹھاں سمجھایا گیا اے۔

کوانٹم مکینکس دی کوپنہاگن وضاحت اندر, ویو فنکشن سبھ توں زیادہ مکمل ویروا ہندا اے جو کسے فیزیکل سسٹم بارے دتا جا سکدا اے۔ شروڈنگر اکیوئیشن پرتِ حل نہ صرف مولیکیولر, ایٹومک, اتے اپّ-ایٹمی سسٹم ہی درساؤندی اے, سگوں میکروسکوپک سسٹم وی درساؤندی اے, ممکن طور تے سارا کائنات وی درساؤندی اے۔^[۴]^:292ff شروڈنگر اکیوئیشن کوانٹم فیلڈ تھیوری سمیت کوانٹم مکینکس دیاں سبھ ایپلیکیشناں پرتِی مرکزی اے, جو سپیشل رلیٹیوٹی نوں کوانٹم مکینکس نال میلدی اے۔ سٹرنگ تھیوری ورگیاں کوانٹم گریوٹی دیاں تھیوریآں وی شروڈنگر اکیوئیشن نوں سدھاردیاں نہیں ہن۔

کوانٹم مکینکس وچ شروڈنگر مساوات سانوں ایہہ دسدی اے کہ کسے پھجکل سسٹم دی کوانٹم سمت ویلے دے مطابق کویں بدلدی اے۔ ایہہ 1925 وچ تیار اتے 1926 وچ آسٹریا دے طبعیاتی سائنسدان ارون شروڈنگر ولوں شائع کیتی گئی۔^[۲] کلاسیکل مکینکس وچ رفتار دی مساوات نیوٹن دے دوجے قنون ( $F = m a$ ) وچ جاں آئلر لگرانجی مساوات دے روپ وچ سانوں دسدی اے کہ اوہ کہڑا رستہ اے جو اک دتا ہویا سسٹم ارمبھک حالتاں دے اک سیٹ ہیٹھ لے لویگا۔ پر کوانٹم مکینکس دی معیاری وضاحت وچ ویوفنکشن سانوں فزیکل سٹیٹ دی ساری جانکاری دندا اے۔ شروڈنگر مساوات نہ صرف ایٹمی, ذرے, اتے سب -ایٹمی کناں دی سمت دی جانکاری دندی اے سگوں میکرو سسٹم, شاید پورے کائنات دی جانکاری وی دندی اے۔

شروڈنگر اکیوئیشن نہ صرف کوانٹم مکینیکل سسٹماں دا مطالعہ کرن اتے اندازا لگاؤن دا اکو اک طریقہ نہیں اے, کیونکہ ہور کوانٹم مکینیکل فارمولا ویونتبندیاں وی ہن, جویں ورنر ہیزنبرگ راہیں پیش کیتا میٹرکس مکینکس, اتے مکھ طور تے رچرڈ فائنمن ولوں ترقی یافتہ کیتی گئی پاتھ انٹگرل فارمولا ویونتبندی۔ پول ڈیراک نے میٹرک مکینکس اتے شروڈنگر اکیوئیشن نوں اکو سنگل فارمولا ویونتبندی وچ شامل کیتا۔

مساوات

وقت-انحصار اکیوئیشن

شروڈنگر اکیوئیشن دا روپ بھوتکی پرحالت اتے انحصار کردا اے (خاص معاملیاں لئی تھلے دیکھو)۔ سبھ توں زیادہ عامَ قسم ویلے تے انحصار شروڈنگر اکیوئیشن ہندی اے, جو وقت نال اتپن ہو راے کسے سسٹم دا اک تذکرہ دندی اے۔:^[۵]^:143

اک ویو فنکشن جو $V = 0$ نال غیر-ساپیکھک (ریلیٹیوسٹک) شروڈنگر اکیوئیشن نوں مطمعن کردا اے۔ دوجے شبداں وچ, ایہہ خالی سپیس راہیں آزاد طور تے سفر کر راے کسے کن نال متعلق ہندا اے۔ ویو فنکشن دا اصلی حصہ اتھے واہیا گیا اے۔

ویلے تے انحصار شروڈنگر اکیوئیشن (عامَ)

$i\hbar {\frac {\partial }{\partial t}}\Psi (\mathbf {r} ,t)={\hat {H}}\Psi (\mathbf {r} ,t)$

جتھے

$i$ خیالی اکائی اے,
$ħ$ گھٹایا ہویا پلینک ستھرانک اے جو ایہہ ہندا اے : $\hbar ={\frac {h}{2\pi }}$ ,
چنہ $\partial / \partial t$ , ٹائم $t$ دے حوالہ وچ اک پارشل ڈیریویٹو ول اشارہ کردا اے,
$Ψ$ (گریک اکھر سائی) کوانٹم سسٹم دا ویو فنکشن ہندا اے,
$r$ اتے $t$ ترتیب وار, ویکٹر اتے ٹائم ہن, اتے
$Ĥ$ ہیملٹونیئن اوپریٹر فنکشن ہندا اے (جو پرحالت اتے انحصار کردیاں ہوئیاں وکھریاں قسماں لیندا ہویا کسے دتے ہوئے ویو فنکشن دی کل توانائی نوں لچھنبدھّ کردا اے)۔

ایہناں تنے قطاراں وچوں ہریک اک ویو فنکشن ہندی اے جو کسے ہارمونک اؤسیلیٹر لئی سمیں-تے-انحصار شروڈنگر اکیوئیشن نوں مطمعن کردا اے۔ کھبے: ویو فنکشن دا اصلی حصہ (نیلے رنگ وچ) اتے خیالی حصہ (لال رنگ وچ)۔ سجے: کسے دتی ہوئی پوزیشن اتے اس ویو فنکشن والے کن نوں کھوجن دی پروبیبلٹی ڈسٹریبیوشن۔ شکھرلیاں دو قطاراں سٹیشنری حالتواں دیاں اداہرناں ہن, جو سٹینڈنگ ترنگاں نال تعلق رکھدیاں ہن۔ تل والی قطار اک اجیہی حالت دی اک اداہرن اے جو کوئی سٹیشنری حالت نہیں ہندی۔ سجا کالم سمجھاؤندا اے کہ کیوں سٹیشنری حالتاں نوں سٹیشنری ہی کیہا جاندا اے۔

سبھ توں زیادہ مشہور اداہرن کسے الیکٹرک فیلڈ وچ (پر کسے چمبکی فیلڈ وچ نہیں: پولی اکویئیشن دیکھو) رفتار شیل کسے سنگل کن واسطے غیر-ساپیکھک (ریلیٹیوسٹک) شروڈنگر اکیوئیشن اے؛^[۶]

ویلے تے انحصار شروڈنگر اکیوئیشن
(سنگل غیر-ساپیکھک (ریلیٹیوسٹک) کن)

$i\hbar {\frac {\partial }{\partial t}}\Psi (\mathbf {r} ,t)=\left[{\frac {-\hbar ^{2}}{2\mu }}\nabla ^{2}+V(\mathbf {r} ,t)\right]\Psi (\mathbf {r} ,t)$

جتھے

$μ$ کن دا گھٹایا ہویا پنج ہندا اے,
$V$ پٹینشل توانائی ہندی اے,
$\nabla 2$ لیپلاسیئن (اک ڈفرینشیئل اوپریٹر) اے, اتے
$Ψ$ ویو فنکشن اے (ہور خالص طور تے, اس حوالہ وچ, اسنوں پجیشن-سپیس ویو فنکشن کیہا جاندا اے)۔ عام بولی وچ, اسدا مطلب اے کل توانائی برابر اے کائنیٹک اینرجی پلسّ پٹینشل اینرجی, پر ہیٹھاں سمجھائے کارناں کرکے رقماں بے پچھان روپ لے لیندیاں ہن۔

شامل ہندے خاص ڈفرینشیئل اوپریٹر دتے ہون تے, ایہہ اک لینیئر پارشل ڈفرینشیئل اکویئیشن ہو جاندی اے۔ ایہہ اک ڈفیوزن اکویئیشن وی ہندی اے, پر ہیٹ اکویئیشن توں الٹ, ایہہ ٹرانزیئینٹ رقم اندر حاضر خیالی یونٹ دتے ہون تے اک ویو اکیوئیشن وی ہندی اے۔

شبد شروڈنگر اکیوئیشن عامَ اکیوئیشن (اپرلا پہلا بوکس) ول وی اشارہ کر سکدی اے, جاں خاص غیر-ساپیکھک (ریلیٹیوسٹک) ورژن (اپرلا دوجا بوکس اتے اسدیاں ویریئیشناں) ول وی۔ عامَ اکیوئیشن سچ مچّ کافی عامَ اکیوئیشن اے, جو سارے کوانٹم مکینکس وچ ہیملٹونیئن لئی وکھ وکھ گنجھل دار سمیکرناں وچ بھر کے ڈیراک اکویئیشن توں لے کے کوانٹم فیلڈ تھیوری تک ہریک چیز واسطے ورتی جاندی اے۔ خاص غیر-ساپیکھک (ریلیٹیوسٹک) ورژن واستوکتا پرتِ اک سنکھیپاتمک لگپگتا اے, جو کئی پرحالات وچ بہت صحیح ہندی اے, پر ہوراں اندر بہت غلط رہندی اے (دیکھو ساپیکھک (ریلیٹیوسٹک) کوانٹم مکینکس اتے ساپیکھک (ریلیٹیوسٹک) کوانٹم فیلڈ تھیوری)۔

شروڈنگر اکیوئیشن اپلائی کرن لئی, سسٹم واسطے اے اوپریٹر سیٹ کیتا جاندا اے, جو سسٹم دے رچنہارے کناں دی کائنیٹک اتے پٹینشل توانائی لئی جمیوار ہندا اے, پھیر شروڈنگر اکیوئیشن وچ پا دتا جاندا اے۔ نتیجن پارشل ڈفرینشیئل اکیوئیشن ویو فنکشن لئی حل کیتی جاندی اے, جو سسٹم بابت اطلاع رکھدی ہندی اے۔

وقت-آزاد اکیوئیشن

اپر درسائی سمیں-تے-انحصار شروڈنگر اکیوئیشن انومانت کردی اے کہ ویو فنکشن سٹینڈنگ ترنگاں رچ سکدے ہن, جہناں نوں سٹیشنری حالتواں (اؤربٹل وی کیہا جاندا اے, جویں ایٹومک اؤربٹلاں جاں مولیکیولر اؤربٹلاں وچ) کیہا جاندا اے۔ ایہہ حالتاں اپنے آپ وچ اہم ہندیاں ہن اتے جیکر سٹیشنری حالتاں نوں شرینیبدھّ کرکے سمجھیا جاوے, تاں کسے وی حالت لئی سمیں-تے-انحصار شروڈنگر اکیوئیشن نوں حل کرنا اسان ہو جاندا اے۔ سٹیشنری حالتاں نوں شروڈنگر اکیوئیشن دی اک آسان قسم راہیں وی درسایا جا سکدا اے جسنوں سماں-آزاد شروڈنگر اکیوئیشن کہندے ہن۔ (ایہہ صرف تاں ورتی جاندی اے جدوں ہیملٹونیئن خود ہی ویلے اتے واضع روپ وچ انحصار نہ کردا ہووے۔ پھیر وی, اس معاملے وچ وی, کل ویو فنکشن اجے وی اک سماں نربھرتا رکھدا ہندا اے۔)

سماں-آزاد شروڈنگر اکیوئیشن (سرو عام)

$\operatorname {\hat {H}} \Psi =E\Psi$

شبداں وچ, اکیوئیشن بیان کردی اے کہ:

جدوں ہیملٹونیئن اوپریٹر کسے ویو فنکشن $&Psi؛$ اتے کریا کردا اے, اتے نتیجہ اوسے ویو فنکشن $Ψ$ دے انوپاتی (پروپوشنل) رہندا اے, تاں $Ψ$ اک سٹیشنری حالت ہندی اے, اتے انپاتک ستھرانک $E$ , حالت $Ψ$ دی توانائی ہندی اے۔

سماں-آزاد شروڈنگر اکیوئیشن ہور تھلے چرچت کیتی گئی اے۔ لینیئر الجبرا نیماولی اندر, ایہہ اکیوئیشن اک آئیگن-ملّ اکویئیشن ہندی اے۔

پہلاں وانگ, سبھ توں زیادہ مشہور پرگٹائ کسے الیکٹرک فیلڈ (پر کوئی چمبکی فیلڈ وچ نہیں) وچ رفتار شیل کسے سنگل کن واسطے غیر-ساپیکھک (ریلیٹیوسٹک) شروڈنگر اکیوئیشن ہندی اے:

سماں-آزاد شروڈنگر اکیوئیشن (سنگل غیر-ساپیکھک (ریلیٹیوسٹک) کن)

$\left[{\frac {-\hbar ^{2}}{2\mu }}\nabla ^{2}+V(\mathbf {r} )\right]\Psi (\mathbf {r} )=E\Psi (\mathbf {r} )$

جسدیاں اپر وانگ پربولیاں ہندیاں ہن۔

ویونتبندی

کوانٹم مکینکس دی اجوکی سمجھ وچ, شروڈنگر اکیوئیشن نوں اسطراں ویونتبند کیتا جا سکدا اے۔^[۷] جیکر ویلے t اتے ویو فنکشن $\Psi (t)$ راہیں دتا جاندا ہووے, تاں کوانٹم مکینکس دی لینیئرٹی صدقہ, ویلے t’ اتے ویو فنکشن ضرور ہی $\Psi (t')=U(t',t)\Psi (t)$ راہیں دتا جانا چاہیدا اے, جتھے $U(t',t)$ اک لینیئر اوپریٹر ہندا اے۔ کیونکہ سماں-اتپتی ضرور ہی ویو فنکشن دے نورم نوں سرکھات کردی ہونی چاہیدی اے, اس توں پتہ چلدا اے کہ $U(t',t)$ لازمی طور تے ویو فنکشناں اتے کریا کر راے اوپریٹراں دے یونائٹری گروپ دا کوئی میمبر ہونا چاہیدا اے۔ اسیں ایہہ وی جاندے ہاں کہ جدوں $t'=t$ ہندا اے, تاں ساڈے کول ضرور ہی $U(t,t)=1$ ہونا چاہیدا اے۔ اسطراں, t دے بہت نزدیک t’ لئی, اوپریٹر $U(t',t)$ دا پھلار کردے ہوئے, اسیں $U(t',t)=1-iH(t'-t)$ لکھ سکدے ہاں جتھے H اک ہرمشن اوپریٹر ہندا اے۔ ایہہ اس حقیقت توں پتہ چلدا اے کہ یونائٹری گروپ نال متعلق لائی الجبرا ہرمشن اوپریٹراں نوں شامل کردا اے۔ سماں-انتر $t'-t$ نوں بہت سوخم حد تک لیندے ہوئے, اسیں شروڈنگر اکیوئیشن حاصل کردے ہاں۔

ہن تک, H صرف اک امورت ہرمشن اوپریٹر ہی ہندا اے۔ پھیر وی, کورسپونڈینس پرنسپل ورتدے ہوئے, ایہہ دکھاؤنا ممکن اے کہ, کلاسیکل حد وچ, H دی ایکسپیکٹیشن ویلیؤ سچ مچّ ہی کلاسیکل توانائی ہندی اے۔ کورسپونڈینس پرنسپل انسرٹنٹی پرنسپل کرکے کوانٹم ہیملٹونیئن دی قسم نوں پوری طرحاں پھکس نہیں کردا, اتے اس کرکے, کوانٹم ہیملٹونیئن دی خالص قسم ضرور ہی انوبھوَ-سدھ طور تے پھکس کیتی جانی چاہیدی اے۔ و

نتیجے

شروڈنگر اکیوئیشن اتے اسدے ہلاں نے فزکس بارے سوچنی وچ اک درار داخل کیتی اے۔ شروڈنگر اکیوئیشن اپنی قسم دی پہلی اکیوئیشن سی, اتے اسدے ہلاں نے اجیاے نتیجیاں ول پریرنا دتی جو وقت لئی بہت ہی اعام اتے بے امید سن۔

کل کائینیٹک اتے ستھتک توانائی

اکویئیشن دی ساری دی ساری قسم اعام جاں امید توں پرے نہیں ہندی, کیونکہ ایہہ توانائی دی سرکھئتا دا پرنسپل ورتدی اے۔ غیر-ساپیکھک (ریلیٹیوسٹک) شروڈنگر اکیوئیشن دیاں رقماں نوں سسٹم دی کل توانائی دے طور تے ویاکھیابدھّ کیتا جا سکدا اے, جو سسٹم کائینیٹک توانائی جماں سسٹم ستھتک توانائی برابر ہندی اے۔ اس حوالہ وچ, ایہہ کلاسیکل فزکس اندرلی توانائی وانگ ہی رہندی اے۔

نردھاریکرن

شروڈنگر اکیوئیشن اندازا لگاؤندی اے کہ جیکر کسے سسٹم دیاں کجھ خاصیتاں ناپیاں جاندیاں ہن, تاں نتیجہ نردھاریکرت ہو سکدا اے, جسدا مطلب اے کہ صرف خاص اجاری ملّ ہی موجود ہو سکدے ہن۔ اک اداہرن توانائی کوانٹائزیشن اے: کسے الیکٹرون دی توانائی کسے ایٹم اندر ہمیشاں ہی کوانٹائزڈ توانائی لیولاں وچوں اک لیول ہندی اے, جو ایٹومک سپیکٹروسکوپی راہیں کھوجیا اک حقیقت اے۔ (توانائی کوانٹائزیشن نوں تھلے چرچت کیتا گیا اے۔ اک ہور اداہرن اینگلر مومینٹم دی کوانٹائزیشن اے۔ ایہہ شروعاتی ایٹم دے بوہر ماڈل وچ اک مانتا سی, پر شروڈنگر اکیوئیشن وچ ایہہ اک اندازا ہندا اے۔

شروڈنگر اکیوئیشن دا اک ہور نتیجہ ایہہ ہندا اے کہ ہریک ناپ کوانٹم مکینکس اندر کوئی کوانٹائز کیتا نتیجہ نہیں دندا۔ اداہرن دے طور تے, پوزیٹرون, مومینٹم, ٹائم, اتے (کجھ پرحالات وچ) توانائی کسے جاری رینج دے آرپار کوئی ملّ رکھدی ہو سکدی اے۔^[۸]^:165–167

ناپ اتے انشچتتا

کلاسیکل مکینکس اندر, اک کن, ہریک پل اتے, اک صحیح صحیح پوزیشن اتے اک صحیح صحیح مومینٹم رکھدا اے۔ ایہہ ملّ نردھارتمک طور تے بدل جاندیاں ہن جویں ہی کن نیوٹن دے نیماں مطابق رفتار کردا اے۔ کوانٹم مکینکس دی کوپنہاگن وضاحت ماتحت, کن صحیح صحیح نردھارتمک خاصیتاں نہیں رکھدے ہندے, اتے جدوں ایہہ خاصیتاں ناپیاں جاندیاں ہن, تاں نتیجہ کسے پروبیبلٹی ڈسٹریبیوشن توں منچااے طور تے کڈھ لیا جاندا اے۔ شروڈنگر اکیوئیشن اندازا لگاؤندی اے کہ پروبیبلٹی وستھار-ونڈاں کی ہندیاں ہن, پر مڈھلے طور تے ہریک ناپ دے صحیح صحیح نتیجے نوں انومانت نہیں کر سکدی۔

ہیزنبرگ دا انسرٹنٹی پرنسپل کوانٹم مکینکس اندر جنمجات ناپ انشچتتا دا کتھن اے۔ ایہہ بیان کردا اے کہ کسے کن دی پوزیشن جنی خالص طور تے معلوم ہندی اے, انی ہی گھٹ خالص طور تے اسدا مومینٹم معلوم ہندا اے, اتے اسدا الٹ وی سچ اے۔

شروڈنگر اکیوئیشن کسے کن دے ویو فنکشن دی (نردھارتمک) اتپتی نوں درساؤندی اے۔ پھیر وی, بھاویں چااے ویو فنکشن خالص طور تے معلوم وی ہووے, تاں وی ویو فنکشن اتے کسے خاص ناپ دا نتیجہ امقررہ رہندا اے۔

کوانٹم ٹنلنگ

کلاسیکل فزکس اندر, جدوں کوئی گیند کسے وڈے پہاڑ دے اتے ہولی ہولی روڑی جاندی اے, تاں ایہہ رک جاندی اے اتے تھلے آؤن لگدی اے, کیونکہ پہاڑ دے دوجے پاسے جان لئی پہاڑ دے شکھر تک چڑن واسطے اس کول لوڑیندی توانائی نہیں ہندی۔ پھیر وی, شروڈنگر اکیوئیشن اندازا لگاؤندی اے کہ اک سوخم پروبیبلٹی ہندی اے کہ گیند پہاڑ دے دوجے پاسے چلی جائیگی, بھاویں شکھر تک جان لئی اس کول بہت ہی گھٹ توانائی ہندی اے جو لوڑیندی توانائی توں بہت گھٹ ہندی اے۔ اسنوں کوانٹم ٹنلنگ کیہا جاندا اے۔ ایہہ توانائی دی ڈسٹریبیوشن نال متعلق اے: بھاویں دی کلپت پوزیشن پہاڑ دے اک پاسے اتے ہندی دسدی اے, پھیر وی اسنوں دوجے پاسے کھوجن دا اک چانس (موقع) ہندا اے۔

ترنگاں دے طور تے کن

غیر-ساپیکھک (غیر-ریلیٹیوسٹک) شروڈنگر اکیوئیشن اکیوئیشن کسے ویو فنکشن نامک پارشل ڈفرینشیئل اکویئیشن دی اک قسم ہندی اے۔ اسلئی, اکثر ایہہ کیہا جاندا اے کہ کن ترنگاں ورگیاں خاصیتاں ورگا ورتاؤ عامطور تے دکھاؤندے ہن۔ کجھ اجوکیاں ویاکھیاواں وچ ایہہ ویروا الٹا دتا گیا ہے- کوانٹم حالت, یانِ کہ, ترنگ, ہی اکو اک اصلی بھوتکی واستوکتا ہندی اے, اتے ڈھشاعراں شرطاں ماتحت ایہہ کن-ورگے ورتاؤ دے لچھن دکھا سکدی اے۔ پھیر وی, بیلینٹین^[۹]^{:Chapter 4, p.99} دکھاؤندا اے کہ اجیہی کوئی وضاحت سمسیاواں-یکت ہندی اے۔ بینلینٹین اشارہ کردا اے کہ جدونکھ کسے بھوتکی ترنگ نوں کسے سنگل کن نال جوڑنا (متعلق کرنا) ترکیوگ ہندا اے, تاں اجے وی صرف اکو شروڈنجر ترنگ مساوات کئی کناں لئی ہندی اے۔ اوہ اشارہ کردا اے کہ:

"جیکر کسے بھوتکی ترنگ فیلڈ نوں کسے کن نال متعلق کیتا جاندا اے, جاں کسے کن نوں کسے ویو-پیکٹ نال پچھانیا جاندا اے, تاں پرسپر کریاواں کردے N کناں نال متعلق پرسپر کریاواں کردیاں N ترنگاں وی عام تنّ-ایامی سپیس اندر ضرور ہونیاں چاہیدیاں ہن۔ پر (4.6) مطابق, اجیہا معاملہ نہیں اے؛ اسدے ستھان تے کسے امورت 3N-ایامی رچنا سپیس اندر اکو ویو فنکشن ہندا اے۔ سائی دی کسے بھوتکی ترنگ دے طور تے گلت-وضاحت عام سپیس وچ صرف تاں ممکن ہندی اے کیونکہ کوانٹم مکینکس دے زیادہتر سانجھے ورتوں اک-کنک حالتاں پرتِ ہندے ہن, جہناں لئی رچنا سپیس اتے عام سپیس آئسومرپھک ہندیاں ہن۔"

دو-سلٹ ڈپھریکشن اوہناں عجیب ورتاواں دی مشہور اداہرن اے جو اجہیاں ترنگاں نیمت طور تے پردرشت کردیاں رہندیاں ہن, جو کناں نال سہج سمجھ دے طور تے متعلق نہیں ہندیاں ہن۔ دوویں سلٹاں توں (اک دوجے دے) اؤورلیپنگ (اپر چڑن والیاں) ترنگاں کجھ ستھاناں وچ پرسپر طور تے ردّ ہو جاندیاں ہن, اتے دوجے ستھاناں (لوکیشناں) تے اک کمپلیکس نمونہ پیدا کرن لئی اک دوجی وچ جڑ جاندیاں ہن۔ سہج سمجھ دے طور تے, سلٹاں اتے کسے سنگل کن نوں فائر کرن توں اس نمونے دی امید کیتی جانی نہیں ہونی چاہیدی, کیونکہ کن اک سلٹ وچ نوں جاں دوجی سلٹ راہیں لنگھنا چاہیدا اے, نہ کہ دوہاں سلٹاں دے کسے کمپلیکس اوورلیپ وچ نوں ہی لنگھنا چاہیدا اے۔

کویں نہ کویں, کیونکہ شروڈنگر اکیوئیشن اک ویو اکویئیشن ہی ہندی اے, اسلئی کوئی سنگل کن جدوں کسے ڈبل-سلٹّ راہیں لنگھن لئی فائر کیتا جاندا اے تاں ایہی نمونہ پردرشت کردا اے (سجے پاسے چتر وچ دیکھو)۔ دھیان دیؤ کہ: استعمال ضرور ہی کئی وار دوہرایا جانا چاہیدا اے تاں جو کمپلیکس نمونہ پیدا ہو سکے۔ بھاویں ایہہ سہج سمجھ ورتکنیک اے, پھیر وی اندازا صحیح رہندا اے؛ خاص کرکے, الیکٹرون ڈپھریکشن اتے نیوٹرون ڈپھریکشن چنگی طرحاں سمجھیاں گئیاں ہن اتے سائنس اتے انجنیئرنگ وچ وڈے پدھر تے ورتیاں گئیاں ہن۔

ڈپھریکشن نال متعلق, کن سپرپجیشن اتے انٹرپھیرینس وی دکھاؤندے ہن۔

سپرپجیشن خاصیت کسے کن نوں دو جاں زیادہ کوانٹم حالتواں دی کسے کوانٹم سپرپجیشن وچ اکو ویلے ہون دی آگیا ددی اے۔ پھیر وی, ایہہ نوٹ کیتا گیا اے کہ کوانٹم مکینکس اندر کوئی کوانٹم حالت دا مطلب اے اوہ پروبیبلٹی, جو کوئی سسٹم, اداہرن دے طور تے, کسے پوزیشن $x$ تے ہو سکدا ہووےگا, نہ کہ سسٹم سچ مچّ ہی پوزیشن $x$ اتے ہووےگا۔ اسدا مطلب ایہہ نہیں اے کہ کن خود ہی اکو ویلے دو کلاسیکل حالتاں وچ ہو سکدا اے۔ سچ مچّ, کوانٹم مکینکس عامطور تے پوری طرحاں ناپ توں پہلاں دیاں خاصیتاں واسطے ملّ حاصل کرن پرتِ ایوگ رہندا اے۔

مینی-ورلڈ وضاحت

ڈبلن وکھے 1952 وچ, ایرون شروڈنجر نے اک لکچر دتا سی, جس وچ اک گل اتے اسنے مذاق دے لہجے وچ اپنے سروتیاں نوں ساودھان کیتا کہ اوہ جو کہن والا اے پگلپن لگ سکدا اے۔ ایہہ اوہ سماں سی, جدوں اسدیاں اتم سمیکرناں وکھ وکھ وکھرے اتہاساں نوں درساؤندیاں دسدیاں سن, جو اک دوجے دا بدل نہیں سن, پر سبھ سچ مچّ ہی اکٹھے واپردے ہن۔ ایہہ کوانٹم مکینکس دی مینی-ورلڈ انٹرپریٹیشن پرتِ ارمبھکاتمک معلوم حوالہ سی۔^[۱۰]

ویو فنکشن دی وضاحت

شروڈنگر اکیوئیشن کسے سسٹم دے ویو فنکشن نوں کیلکلیٹ کرن اتے کویں کوئی سسٹم وقت وچ رفتار شیل طور تے بدلدا اے, نوں کیلکلیٹ کرن پرتِ اک رستہ مہیا کرواؤندی اے۔ پھیر وی, شروڈنگر اکیوئیشن سدھے طور تے نہیں کہندی کہ ویو فنکشن اصل وچ کی ہندا اے۔ کوانٹم مکینکس دیاں ویاکھیاواں سوالاں دی گل کردیاں ہن جویں ویو فنکشن, جو واستوکتا لئی جمیوار ہندا اے, اتے پریوگک ناپاں درمیان کی تعلق ہندا اے۔

اک اہم پہلو شروڈنگر اکیوئیشن اتے ویو فنکشن کولیپس درمیان تعلق اے۔ پراتناتمک کوپنہاگن وضاحت اندر, کن ویو فنکشن کولیپس دوران, جس وچ اوہ پوری طرحاں الگ ہی ورتاؤ کردے ہن, نوں چھڈّ کے شروڈنگر اکیوئیشن دی پالنا کردے ہن۔ کوانٹم ڈیکوہرنس تھیوری دی کھوج نے بدلویں درشٹیکوناں (جویں ایوریٹ مینی-ورلڈز وضاحت اتے مطابق اتہاساں) نوں آگیا دتی, جتھے کہ شروڈنگر اکیوئیشن ہمیشاں ہی کھری اتردی اے, اتے ویو فنکشن کولیپس شروڈنگر اکیوئیشن دے کسے نتیجے دے طور تے ویاکھئت کیتا جانا چاہیدا اے۔

تریخی پچھوکڑ اتے ترقی

پرکاش دی میکس پلینک دی کوانٹائزیشن (بلیک بوڈی ریڈیئیشن دیکھو) دی پالنا کردے ہوئے, البرٹ آئینسٹائین نے پلینک دے کوانٹا نوں پھوٹوناں دے ہون وجوں ویاکھئت کیتا, جو پرکاشی کن ہندے ہن, اتے پیش کیتا کہ کسے پھوٹون دی توانائی اسدی پھریکئینسی دے انوپاتی ہندی اے, جو ترنگ-کن ڈیولٹی دے پہلے لچھناں وچوں اک سی۔ کیونکہ توانائی اتے مومینٹم اسے طریقے نال متعلق ہندے ہن جویں پھریکئینسی اتے ویونمبر, سپیشل رلیٹیوٹی وچ متعلق ہندے ہن, تاں استوں پتہ چلدا اے کہ, کسے پھوٹون دا مومینٹم $p$ اسدی ویولینتھ $λ$ دے انوپاتی ہندا اے, جاں اسدے ویونمبر $k$ دے انوپاتی (پروپوشنل) ہندا اے:

p={\frac {h}{\lambda }}=\hbar k,

جتھے $h$ پلینک دا ستھرانک اے۔ لئس ڈی بروگلِ نے نظریاتی کیتا کہ سارے کناں لئی ایہہ سچ رہندا اے, بھاویں الیکٹروناں ورگے پنج والے کن ہی کیوں نہ ہون۔ اسنے دکھایا کہ, ایہہ مندے ہوئے کہ پدارتھک ترنگاں اپنے کن ورودھیساتھیاں دے نال نال سنچارت ہندیاں ہن, الیکٹرون, سٹینڈنگ ترنگاں رچدے ہن, جسدا مطلب اے کہ صرف کجھ اجاری روٹیشنل پھریکئینسیاں ہی نیوکلیئس دوآلے کسے ایٹم لئی پروانت ہندیاں ہن۔^[۱۱]

ایہہ کوانٹائزڈ اؤربٹ ڈسکریٹ (اجاری) توانائی پدھراں نال متعلق ہندے ہن, اتے ڈی بروگلی نے اینرجی لیولاں لئی بوہر ماڈل نوں دوبارہ پیدا کیتا۔ بوہر ماڈل اس اکیوئیشن مطابق اینگلر مومینٹم $L$ دی منی ہوئی کوانٹائزیشن اتے مشتمل سی:

L=n{h \over 2\pi }=n\hbar

ڈی بروگلی مطابق الیکٹرون نوں کسے ترنگ راہیں درسایا جاندا اے اتے ترنگ-لمبائیآں دا اک مکمل نمبر ضرور ہی الیکٹرون دے اؤربٹ دے گھیرے دے نال نال فٹ ہونا چاہیدا اے:

n\lambda =2\pi r.\,

ایہہ نظریہ اردھ-ویاس (ریڈیئس) $r$ والے کسے چکری اؤربٹ دے نال نال, لازمی طور تے اک ایام وچ الیکٹرون ترنگ نوں محدود رکھدا اے۔

1921 وچ, ڈی بروگلی توں پہلاں, ارتھر چی لنّ نے شیکاگو دی یونیورسٹی وکھے, ہن ڈی بروگلی تعلق کاے جان والے تعلق نوں ویونتبند کرن لئی ساپیکھک (ریلیٹیوسٹک) اورجا-مومینٹم 4-ویکٹر دی تکمیل اتے مشتمل اوہی ترک ورتیا سی۔^[۱۲] برگولِ توں الٹ, لنّ اجیہی ڈفرینشیئل اکیوئیشن فارمولا ویونتبند کرن گیا جسنوں ہن شروڈنگر اکیوئیشن دے طور تے جانیا جاندا اے, اتے ہائیڈروجن ایٹم لئی اسدے توانائی آئیگن-ملّاں نوں حل کرن تک گیا۔ بدقسمتی نال, اسدا پیپر فزیکل ریویؤ راہیں ردّ کر دتا گیا, جویں کیمن راہیں دوبارہ گنیا گیا۔^[۱۳]

ڈی بروگلِ دے وچاراں دی پالنا کردے ہوئے, بھوتک سائنسدان پیٹر ڈبائ نے اک اکدم ٹپنی کیتی کہ جیکر کن ترنگاں دی طرحاں ورتاؤ کردے ہون, تاں اوہ اسانی نال کسے قسم دی ویو اکیوئیشن دی پالنا کردے ہونے چاہیدے ہن۔ ڈیبائ دی ٹپنی توں پریرنا لے کے شروڈنجر نے الیکٹرون لئی اک ڈھکویں 3-ڈائمینشنل ویو اکویئیشن کھوجن دا فیصلہ کر لیا۔ اسدا مرگ فلسفہ ولیئم روون ہیملٹن دی مکینکس اتے اؤپٹکس درمیان تلتا (اینالوگی) نے کیتا, جس دے معائنہ وچ ایہہ سکینتبدھّ کیتا ہویا سی کہ, اؤپٹکس دی زیرِ-ترنگلمبائی سیما کسے مکینیکل سسٹم نال ملدی جلدی ہے- پرکاش کرناں دے وکرت پتھ تکھے بن جاندے ہن جو پھارمٹ دے پرنسپل دی پالنا کردے ہن, جو لیسٹ ایکشن اصول دا اک تلّ (اینالوگ) اے۔^[۱۴]اسدے ترک دا اک اجوکا ورژن تھلے پھیر توں پیدا کیتا گیا اے۔ اسدے ولوں کھوجی گئی اکیوئیشن ایہہ اے:^[۱۵]

i\hbar {\frac {\partial }{\partial t}}\Psi (\mathbf {r} ,\,t)=-{\frac {\hbar ^{2}}{2m}}\nabla ^{2}\Psi (\mathbf {r} ,\,t)+V(\mathbf {r} )\Psi (\mathbf {r} ,\,t).

پھیر وی, اوس وقت تک, ارنالڈ سومرفیلڈ نے ساپیکھک (ریلیٹیوسٹک) سدھاراں صدقہ بوہر ماڈل نوں سدھار دتا سی۔^[۱۶]^[۱۷] شروڈنجر نے (قدرتی یونٹاں وچ) کسے کولومب پٹینشل اندر کلیئن-جورڈن اکویئیشن دے طور تے ہن جانی جاندی اکیوئیشن نوں کھوجن لئی ساپیکھک (ریلیٹیوسٹک) مومینٹم تعلق دی ورتوں کیتی سی:

\left(E+{e^{2} \over r}\right)^{2}\psi (x)=-\nabla ^{2}\psi (x)+m^{2}\psi (x).

اسنے اس ساپیکھک (ریلیٹیوسٹک) اکیوئیشن دیاں سٹینڈنگ ترنگاں کھوجیاں, پر ساپیکھک (ریلیٹیوسٹک) سدھار سومرفیلڈ دے فارمولے نال اسہمت راے۔ مایوس ہو کے, اسنے اپنے حساب –کتاباں نوں پرے رکھ دتا اتے اپنے آپ نوں دسمبر 1925 وچ اک بند پہاڑی کیبن وچ تنہا کر لیا۔^[۱۸] جدونکھ اس کیبن اتے, شروڈنگر اکیوئیشن نے فیصلہ کیتا کہ اسدیاں شروعاتی غیر-ساپیکھک کیلکلیشناں چھپن لئی اتم ہون یوگ ہن, اتے مستقبل لئی ساپیکھک سدھاراں دی مسئلہ نوں چھڈّ دتا ہائیڈروجن واسطے ڈفرینشیئل مساوات حل کرن وچ پیش آؤندیاں کٹھنائیاں دے باو جود (اسنے اپنے دوست گنتشعورت حرمن ویئل توں مدد منگی سی)^[۱۹]^:3) شروڈنجر نے دکھایا کہ ویو اکیوئیشن دے اسدے غیر-ساپیکھک ورژن نے1926 وچ چھپے اک پیپر وچ ہائیڈروجن دیاں صحیح سپیکٹرل اورجاواں پیدا کیتیاں سن۔^[۱۹]^:1^[۲۰] اکیوئیشن وچ, شروڈنجر نے پروٹون راہیں بنائی کسے پٹینشل ویلّ $V$ وچ رفتار شیل کسے ترنگ $Ψ (x, t)$ دے طور تے کسے ہائیڈروجن ایٹم دے الیکٹرون نوں ٹریٹ کرکے ہائیڈروجن سپیکٹرل سیریز دا حساب لگایا سی۔ اس حساب-کتاب نے خالص طور تے بوہر ماڈل دے توانائی لیولاں نوں دوبارہ پیدا کیتا سی۔ اک پیپر وچ, شروڈنجر نے خود اس مساوات نوں اسطراں سمجھایا سی:

“	پہلاں توں ہی … نام لیا گیا سائی-فنکشن ۔.۔. ہن ناپ نتیجیاں دی پروبیبلٹی انمات کرن لئی مطلب رکھدا اے۔ اس وچ مستقبل دیاں امیداں تے اصولی طور تے مشتمل پربھر لئی حاصل جوڑ جڑے ہندے ہن۔	”
—ایرون شروڈنجر^[۲۱]

اس 1926 دے پیپر نوں اتشاہپوروج آئینسٹائین راہیں حمایت ملیا, جسنے پدارتھک-ترنگاں نوں قدرت دے اک سہج-سمجھ والی تصویر دے طور تے دیکھیا, جو ہیزنبرگ دے میٹرکس مکینکس توں الٹ سی, جسنوں اسنے ضرورت توں زیادہ رسمی منیا۔^[۲۲]

شروڈنگر اکیوئیشن $Ψ$ دے سبھاء دا ویروا دندی اے پر اسدی فطرت بارے کجھ نہیں دسدی۔ شروڈنجر نے اپنے چوتھے پیپر وچ اک چارج ڈینسٹی دے طور تے اسدی وضاحت کرن دی کوشش کیتی, پر ناکام رہا۔^[۲۳]^:219

1926 وچ, شروڈنجر دے چوتھے اتے آخری پیپر دے چھپن توں صرف کجھ دناں بعد ہی, میکس بورن نے سپھلتاپوروک پروبیبلٹی اینپلیٹیوڈ دے طور تے $Ψ$ دی وضاحت کیتی, جسدا خالص سکئیئر پروبیبلٹی ڈینسٹی برابر ہندا اے۔^[۲۳]^:220 شروڈنجر, بھاویں, ہمیشاں ہی- زیادہتر آئینسٹائین وانگر- کسے سٹیٹسٹیکل جاں پروبیبلسٹک نظریہ دا اسدے نال متعلق انرنتراواں سمیت خلاف کردا رہا سی, جسدا (آئینسٹائین دا) یعقین سی کہ کوانٹم مکینکس کسے پچھے چھپی ڈٹرمنسٹک تھیوری پرتِ اک سٹیٹسٹیکل سنکھیپیؤ ہے- اتے کدے وی کوپنہاگن وضاحت نال میل ملاپ نہ کیتا۔^[۲۴]

لئس ڈی بروگلی نے اپنے بعد دے سالاں وچ ڈی بروگلو-بوہم تھیوری ترقی یافتہ کردے ہوئے, کسے انوپاتی ستھرانک راہیں کمپلیکس ویو فنکشن نال جڑیا اک اصلی ملّ والا ویو فنکشن پیش کیتا۔

کناں لئی ترنگ مساوات

شروڈنگر اکیوئیشن اک ڈفیوزن مساوات ہندی اے,^[۲۵] جسدے حل اجیاے فنکشن ہندے ہن جو ترنگ-ورگیاں گتیاں درساؤندے ہن۔ فزکس اندرلیاں ترنگ سمیکرناں (ویو اکئیشناں) عامطور تیہور بھوتکی اصولاں توں ویونتبند ہندیاں ہن- سٹرنگاں اتے اتے مادہ وچ مکینیکل کمپناں لئی ویو اکیوئیشن نوں نیوٹن دے نیماں توں ویونتبند کیتا جا سکدا اے, جتھے ویو فنکشن مادہ دا وستھاپن پرسعنصر کردا اے, اتے میکسویلّ اکئیشناں توں الیکٹرومیگنیٹک ترنگاں ویونتبند کیتیاں جا سکدیاں ہن, جتھے ویو فنکشن الیکٹرک اتے چمبکی فیلڈاں ہندے ہن۔ دوجے پاسے, شروڈنگر اکیوئیشن لئی ادھار, سسٹم دی توانائی ہندی اے اتے اک وکھری کوانٹم مکینکس دا سوے-سدھ اصول ہندا اے: ویو فنکشن سسٹم دا اک ویروا ہندا اے۔^[۲۶] اسطراں شروڈنگر اکیوئیشن اپنے آپ وچ اک نویں دھارنا ہندی اے؛ جویں پھیئنمن اس بارے کہندا اے:

“	اسیں اوہ (مساوات) کتھوں حاصل کیتی؟ کتوں وی نہیں۔ اسنوں کتوں اجیہی چیز توں ویونتبند کرنا ممکن ہی نہیں اے جو چیز وی تسیں جاندے ہووو۔ ایہہ شروڈنجر دے دماغ دی اپج اے۔	”
—رچرڈ پھیئنمن^[۲۷]

اکیوئیشن دی بنیاد کلاسیکل توانائی سرکھئتا اتے مشتمل کسے ریکھک ڈفرینشیئل اکیوئیشن ہون پرتِ رچی گئی اے, اتے ایہہ ڈی بروگلی تعلقاں دے مطابق اے۔ حل ویو فنکشن $ψ$ اے, جو اوہ ساری جانکاری رکھدا اے جو وی سسٹم بابت جانیا جا سکدا ہووے۔ کوپنہاگن وضاحت اندر, $ψ$ دا موڈولس اجیاے کناں دی پروبیبلٹی نال متعلق ہندا اے جو, وقت دے کسے پل اتے کسے سپیشیئل (مقامی) بنتر وچ ہدے ہن۔ $ψ$ لئی اکیوئیشن نوں حل کرن دی ورتوں ایہہ انومانت کرن لئی کیتی جا سکدی اے کہ اک دوجے نال اتے خاص پٹینشل دے اثر ماتحت کن کویں ورتاؤ کرنگے۔

شروڈنگر اکیوئیشن اصولی طور تے ڈی بروگلی پرسوچ توں ترقی یافتہ کیتی گئی سی, جو اک اجیہی ویو اکیوئیشن اے جو کناں نوں درسا سکدی اے,^[۲۸] اتے غیر-رسمی طور تے اگے لکھے حصیاں وچ دکھائے وانگ رچی جا سکدی اے۔^[۲۹] شروڈنگر اکیوئیشن دے اک ہور زیادہ ٹھوس تذکرہ لئی Resnick et al۔^[۳۰] وی دیکھو۔

توانائی سرکھئتا نال انوکولتا

کسے کن دی کل توانائی $E$ کائینیٹک توانائی $T$ اتے ستھتک توانائی $V$ دے جوڑ برابر ہندی اے, ایہہ جوڑپھل کلاسیکل مکینکس اندر ہیملٹونیئن $H$ لئی اکثر ورتی جاندی مساوات وی اے:

E=T+V=H\,\!

واضع روپ وچ, اک ایام وچ پوزیشن $x$ , پنج $m$ اتے مومینٹم $p$ اتے پٹینشل توانائی $V$ والے کسے کن لئی, جو عامطور تے پوزیشن اتے ٹائم $t$ نال بدلدا رہندا اے:

E={\frac {p^{2}}{2m}}+V(x,t)=H.

تن ایاماں لئی, پوزیشن ویکٹر $r$ اتے مومینٹم ویکٹر $p$ ضرور ہی ورتے جانے چاہیدے ہن:

E={\frac {\mathbf {p} \cdot \mathbf {p} }{2m}}+V(\mathbf {r} ,t)=H

ایہہ فارمولا ویونتبندی کناں دے کسے وی پھکس کیتے نمبر تک ودھائی جا سکدی اے: سسٹم دی کل توانائی پھیر کناں دیاں کل کائینیٹک اورجاواں اتے کل پٹینشل اورجاواں دا جوڑ ہندا اے, جو پھیر توں ہیملٹونیئن بن جاندا اے۔ پھیر وی, کناں درمیان پرسپر کریاواں ہو سکدیاں ہن (اک $N$ -بوڈی مسئلہ), تاں جو پٹینشل توانائی $V$ کناں دی سپیشیئل بنتر بدلن نال بدل جاندی اے, اتے ممکن طور تے ویلے دے بدلن نال وی بدل جاندی اے۔ پٹینشل توانائی, عامطور تے, ہریک کن لئی وکھریاں پٹینشل اورجاواں دا جوڑ نہیں ہندی, سگوں ایہہ کناں دیاں ساریاں سپیشیئل پوزیشناں دا اک فنکشن ہندی اے۔ واضع روپ وچ:

E=\sum _{n=1}^{N}{\frac {\mathbf {p} _{n}\cdot \mathbf {p} _{n}}{2m_{n}}}+V(\mathbf {r} _{1},\mathbf {r} _{2}\cdots \mathbf {r} _{N},t)=H\,\!

ریکھکتا (لینیئرٹی)

آسان ترین ویو فنکشن اس قسم دی اک پلین ویو ہندا اے:

\Psi (\mathbf {r} ,t)=Ae^{i(\mathbf {k} \cdot \mathbf {r} -\omega t)}\,\!

جتھے؛

$A$ اینپلیٹیوڈ ہندا اے,
$k$ ویو-ویکٹر ہندا اے, اتے
$ω$ پلین ویو دی اینگلر پھریکئینسی ہندی اے۔

عامطور تے, بھوتکی پرحالات پلین ترنگاں راہیں خالص طور تے نہیں درسائیاں جاندیاں, اسلئی سرو سدھاریکرن لئی سپرپجیشن پرنسپل دی لوڑ پیندی اے؛ سائینسوآئڈل پلین ترنگاں دی سپرپجیشن راہیں کوئی وی ترنگ بنائی جا سکدی اے۔ اسلئی جیکر اکیوئیشن لینیئر ہووے, تاں پلین ترنگاں دا اک لینیئر میل وی اک پروانت حل ہندا اے۔ اسے کرکے اک لازمی اتے وکھری لوڑ ایہہ رہندی اے کہ شروڈنگر اکیوئیشن اک لینیئر ڈفرینشیئل اکویئیشن راے۔

اجاری $k$ لئی, جوڑ, پلین ترنگاں دی اک سپرپجیشن ہندا اے:

\Psi (\mathbf {r} ,t)=\sum _{n=1}^{\infty }A_{n}e^{i(\mathbf {k} _{n}\cdot \mathbf {r} -\omega _{n}t)}\,\!

کجھ اصلی اینپلیٹیوڈ گنانکاں $A n$ لئی, اتے جاری $k$ لئی, جوڑ اک انٹگرل بن جاندا اے, جو کسے مومینٹم سپیس ویو فنکشن دا پھوریئر ٹرانسپھورم ہندا اے:^[۳۱]

\Psi (\mathbf {r} ,t)={\frac {1}{({\sqrt {2\pi }})^{3}}}\int \Phi (\mathbf {k} )e^{i(\mathbf {k} \cdot \mathbf {r} -\omega t)}d^{3}\mathbf {k} \,\!

جتھے $d 3 k = dk x dk y dk z$ $k$ -سپیس وچ ڈفرینشیئل وولیؤم ایلیمینٹ ہندا اے, اتے انٹگرل ساری $k$ -سپیس تے قبضہ کر لیندے ہن۔ مومینٹم ویو فنکشن $Φ (k)$ انٹیگرینڈ وچ پیدا ہو جاندے ہن کیونکہ پوزیشن اتے مومینٹم سپیس ویو فنکشن اک دوجے دے پھوریئر ٹرانسپھورم ہی ہندے ہن۔

ڈی-برگولِ تعلقاں نال انوکولتا

اکیوئیشن دی لائیٹ کوانٹا پرسوچ (1905) بیان کردی اے کہ کسے فوٹون دی توانائی $E$ متعلق پرکاش دے کوانٹم ویو-پیکٹ دی فریکیوئینسی $ν$ (جاں اینگلر فریکیوئینسی, $ω = 2 π ν$ ) دے انوپاتی ہندا اے:

E=h\nu =\hbar \omega \,\!

اسیتراں ڈی بروگلی دی پرسوچ (1924) بیان کردی اے کہ کوئی وی کن کسے ترنگ نال جوڑیا (سبدھت کیتا) جا سکدا اے, اتے کن دا مومینٹم $p$ اک ایام وچ اجیہی کسے ترنگ دی ترنگ-لمبائی $λ$ دے اس راہیں الٹ-انپاتی ہندا اے (جاں ویو-نمبر, $k = 2π / λ$ دے انوپاتی ہندا اے):

p={\frac {h}{\lambda }}=\hbar k\;,

جدونکھ تن ایاماں اندر, ویولینتھ $λ$ ویو-ویکٹر $k$ دے ملّ نال متعلق ہندی اے:

\mathbf {p} =\hbar \mathbf {k} \,,\quad |\mathbf {k} |={\frac {2\pi }{\lambda }}\,.

پلینک-آئینسٹائین اتے ڈی بروگلِ تعلق توانائی دے ویلے نال, اتے سپیس دے مومینٹم نال, درمیان گہرے سمپرکاں تے روشنی پاؤندے ہن, اتے ویو-پارٹیکل ڈیولٹی سمیکرنبدھّ کردے ہن۔ مشق وچ, $ħ = 1$ والیاں قدرتی یونٹاں ورتیاں جاندیاں ہن, کیونکہ ڈی بروگلی سمیکرناں آئڈینٹٹیاں تک گھٹ جاندیاں ہن: تے مومینٹم, ویو-آبادی, توانائی اتے پھریکئینسی نوں آپس وچ وٹا کے ورت ہون دی آگیا دندیاں ہن, تاں جو ماتراواں دی نقل (ڈپلیکیشن) روکی جا سکے, اتے متعلق ماتراواں دے ایاماں دی گنتی گھٹ سکے۔ جان-پچھان لئی اس لیکھ وچ اجے وی SI یونٹاں ورتیاں گئیاں ہن۔

شروڈنجر دی گہری سمجھ,^{[حوالہ درکار]} نے 1925 دے اخیر وچ, ایہناں تعلقاں نوں ورتدے ہوئے اک کمپلیکس فیز پھیکٹر دے طور تے لوسے پلین ویو دے فیز نوں سمیکرنبدھّ کرنا سی:

\Psi =Ae^{i(\mathbf {k} \cdot \mathbf {r} -\omega t)}=Ae^{i(\mathbf {p} \cdot \mathbf {r} -Et)/\hbar }

اتے ایہہ محسوس کرنا سی۔ کہ پہلے درجے دے انشک ڈیریوٹو ایہہ سن: سپیس دے حوالہ وچ:

\nabla \Psi ={\dfrac {i}{\hbar }}\mathbf {p} Ae^{i(\mathbf {p} \cdot \mathbf {r} -Et)/\hbar }={\dfrac {i}{\hbar }}\mathbf {p} \Psi

ویلے دے حوالہ وچ:

{\dfrac {\partial \Psi }{\partial t}}=-{\dfrac {iE}{\hbar }}Ae^{i(\mathbf {p} \cdot \mathbf {r} -Et)/\hbar }=-{\dfrac {iE}{\hbar }}\Psi

کوانٹم مکینکس دا اک ہور سوے-سدھ اصول ایہہ اے کہ سارے اؤبزرویبلاں نوں لینیئر ہرمشن اوپریٹراں نال پرسعنصر کیتا جاندا اے جو ویو فنکشن اتے کریا کردے ہن, اتے اوپریٹر دے آئیگن-ملّ اوہ ملّ ہندے ہن جو اؤبزرویبل لیندے ہن۔ پچھلے ڈیریوٹو, سماں ڈیریویٹو نال متعلق ہندے ہوئے توانائی اوپریٹر دے مطابق ہندے ہن,

{\hat {E}}\Psi =i\hbar {\dfrac {\partial }{\partial t}}\Psi =E\Psi

جتھے $E$ توانائی آئیگنملّ ہندے ہن, اتے ہیٹھاں دتے سپیشیئل ڈیریویٹواں (گریڈیئنٹ $\nabla$ ) نال متعلق مومینٹم اوپریٹر ہندے ہن, جتھے $p$ مومینٹم آئیگنملاں دا اک ویکٹر ہندا اے۔

{\hat {\mathbf {p} }}\Psi =-i\hbar \nabla \Psi =\mathbf {p} \Psi

جتھے $p$ , مومینٹم آئیگن-ملّاں دا اک ویکٹر ہندا اے۔ اپروکت وچ, "ہیٹ" ( $ˆ$ ) اشارہ کردا اے کہ ایہہ اؤبزرویبل اوپریٹر ہندے ہن, آسان طور تے عام سنکھیاواں جاں ویکٹر نہیں ہندے۔ توانائی اتے مومینٹم اوپریٹر ڈفرینشیئل اوپریٹر ہندے ہن, جدونکھ پٹینشل توانائی فنکشن $V$ صرف اک گناتمک حصہ ہی ہندا اے۔

کلاسیکل توانائی سرکھئتا اکیوئیشن وچ توانائی اتے مومینٹم اوپریٹراں نوں بھردے ہوئے ایہہ اوپریٹر حاصل ہندا اے:

E={\dfrac {\mathbf {p} \cdot \mathbf {p} }{2m}}+V\quad \rightarrow \quad {\hat {E}}={\dfrac {{\hat {\mathbf {p} }}\cdot {\hat {\mathbf {p} }}}{2m}}+V

اسلئی ٹائم اتے سپیس دے حوالہ وچ ڈیریویٹواں دے اصولاں وچ, ویو فنکشن $Ψ$ اتے اس اوپریٹر دی کریا نے شروڈنجر نوں ترنت ہی اسدی اکیوئیشن پرتِ پریرنا دتی:^{[حوالہ درکار]}

i\hbar {\dfrac {\partial \Psi }{\partial t}}=-{\dfrac {\hbar ^{2}}{2m}}\nabla ^{2}\Psi +V\Psi

ترنگ-کن دوہریپن نوں ایہناں اکئیشناں توں اگے لکھے طریقے نال اکٹھا کیتا جا سکدا اے۔ کائینیٹک توانائی $T$ مومینٹم $p$ دے طبقہ نال متعلق ہندی اے۔ جویں ہی کن دا مومینٹم ودھ جاندا اے, اوویں ہی کائینیٹک توانائی ہور تیزی نال ودھ جاندی اے, پر کیونکہ ویو-نمبر $| k |$ ودھ جاندا اے, اسلئی نال ترنگ-لمبائی $λ$ گھٹ جاندی اے۔

عام سکیلر اتے ویکٹر ماتراواں (اوپریٹر نہیں) دی بولی وچ:

\mathbf {p} \cdot \mathbf {p} \propto \mathbf {k} \cdot \mathbf {k} \propto T\propto {\dfrac {1}{\lambda ^{2}}}

کائینیٹک توانائی دوجی سپیشیئل ڈیریویٹواں دے انوپاتی وی ہندی اے, اسلئی ایہہ ایہناں اوپریٹراں دے اصولاں وچ, ترنگ دے کرویچر دے میگنیٹیوڈ دے وی انوپاتی ہندی اے:

{\hat {T}}\Psi ={\frac {-\hbar ^{2}}{2m}}\nabla \cdot \nabla \Psi \,\propto \,\nabla ^{2}\Psi \,.

جویں جویں کرویچر ودھدا جاندا اے, ترنگ دا اینپلیٹیوڈ پوزٹو اتے نیگٹو درمیان ہور تیزی نال تبدیل ہندا جاندا اے, اتے ترنگ-لمبائی نوں وی گھٹاؤندا جاندا اے۔ اسلئی مومینٹم اتے ترنگ-لمبائی درمیان الٹ تعلق, کن ولوں رکھی جاندی توانائی دے مطابق ہندا اے, اتے اسلئی کن دی توانائی کسے ترنگ, نال اسے گنتک فارمولا ویونتبندی وچ سارا رابطہ رکھدی اے۔^[۲۸]

ترنگ اتے کن رفتار

ویوپیکٹ لوکلائزیشن دے ودھ راے لیول, جہناں دا مطلب اے کہ کن اک ہور زیادہ ستھانبدھّ پوزیشن رکھدا اے۔

حد ħ → 0 وچ, کن دی پوزیشن اتے مومینٹم خالص طور تے معلوم بن جاندے ہن۔ ایہہ کلاسیکل کن دے سامان اے۔

شروڈنجر نے منگ کیتی کہ پوزیشن $r$ دے نیڑے, $k$ نزدیک ویو-ویکٹر نال, اک ویو-پیکٹ حل, کلاسیکل مکینکس راہیں مقرر وکرت رستے دے نال نال رفتار کرنگے جو $k$ وچ پھلار لئی گھٹ ویلے واسطے ہندے ہن (اتے اسے کرکے ولوسٹی وچ) جو $r$ وچ پھیلے پھلار نوں کافی حد تک ودھاؤن لئی نہیں ہندے۔ کیونکہ, $k$ وچ کسے دتے ہوئے پھلار لئی, ولوسٹی وچ پھلار پلینک دے ستھرانک $ħ$ پرتِ انوپاتی ہندے ہن, تاں ایہہ کدے کدے کیہا جاندا اے کہ $ħ$ دے صفر تک پہنچن تک دی حد وچ, کلاسیکل مکینکس دیاں اکئیشناں کوانٹم مکینکس توں دوبارہ سٹور ہو جاندیاں ہن۔^[۳۲] ایہہ حد کویں اتے کہڑے معاملیاں وچ لینی چاہیدی اے, بہت ساودھانی منگدی اے۔

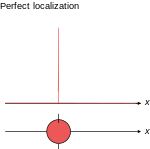
محدود چھوٹی ترنگلمبائی صفر ہو راے $ħ$ سامان ہندی اے کیونکہ ایہہ کن دی مقررہ پوزیشن پرتِ ویو-پیکٹ لوکلائزیشن ودھاؤن دا محدود معاملہ ہندا اے (سجے پاسے والی تصویر دیکھو)۔ پوزیشن اتے مومینٹم لئی [[ہیزنبرگ انشچتتا اصول[[ ورتدے ہوئے, پوزیشن اتے مومینٹم وچ انشچتتا زیرو بن جاندی اے جیوں ہی $ħ \to 0$ پہنچدا اے:

\sigma (x)\sigma (p_{x})\geqslant {\frac {\hbar }{2}}\quad \rightarrow \quad \sigma (x)\sigma (p_{x})\geqslant 0\,\!

جتھے $σ$ , $x$ اتے $p x$ (اتے اسیتراں $y$ اتے $z$ -سمتاں واسطے وی) وچ (روٹ مین سکئیئر) ناپ انشچتتا درساؤندا اے, جسدا مطلب اے پوزیشن اتے مومینٹم اس حد وچ صرف کسے منچاہی شدھتا تک ہی معلوم ہو سکدے ہن۔

شروڈنگر اکیوئیشن اپنی جنرل قسم,

i\hbar {\frac {\partial }{\partial t}}\Psi \left(\mathbf {r} ,t\right)={\hat {H}}\Psi \left(\mathbf {r} ,t\right)\,\!

وچ ہیملٹن-جیکبی اکویئیشن (HJE) نال نزدیکی طور تے متعلق ہندی اے؛

{\frac {\partial }{\partial t}}S(q_{i},t)=H\left(q_{i},{\frac {\partial S}{\partial q_{i}}},t\right)\,\!

جتھے؛

$S$ ایکشن ہندا اے, اتے
$H$ ہیملٹونیئن فنکشن ہندا اے (اوپریٹر نہیں ہندا)۔

اتھے سرو عام کیتے ہوئے نردیشانک $q i$ , $i = 1, 2, 3$ لئی (ہیملٹن-جیکبی اکیوئیشن دے حوالہ وچ ورتے جاندے) کارٹیزیئن نردیشانکاں (کوآرڈینیٹاں) وچ $r = (q 1, q 2, q 3) = (x, y, z)$ ^[۳۲] دے طور تے پوزیشن پرتِ سیٹ کیتے جا سکدے ہن۔

\Psi ={\sqrt {\rho (\mathbf {r} ,t)}}e^{iS(\mathbf {r} ,t)/\hbar }\,\!

نوں شروڈنگر اکیوئیشن وچ بھردے ہوئے,

جتھے $ρ$ پروبیبلٹی ڈینسٹی ہندی اے, اتے نتیجن اکیوئیشن وچ $ħ \to 0$ والی حد لیندے ہوئے, ہیملٹن-جیکبی اکیوئیشن ملدی اے۔

نتیجے ایہہ رہندے ہن:

کسے کن دی رفتار, جو شروڈنگر اکیوئیشن پرتِ (گھٹ ترنگ لمبائی والے) ویو پیکٹ ہلاں راہیں درسائی جاندی ہووے, رفتار دی ہیملٹن-جیکبی اکیوئیشن راہیں وی درسائی جاندی اے۔
شروڈنگر اکیوئیشن ویو فنکشن شامل کردی اے, اسلئی اسدے ویو پیکٹ حل توں مطلب اے کہ کسے (کوانٹم) کن دی پوزیشن ترنگ پھرنٹاں وچ دھندلے طور تے پھیلی ہندی اے۔ اسدے برخلاف, ہیملٹن-جیکبی اکیوئیشن مقررہ پوزیشن اتے مومینٹم والے کسے (کلاسیکل) کن اتے لاگوُ ہندی اے, نہ کہ سارے سمیاں (وکرت رستیاں) اتے پوزیشن اتے مومینٹم نردھارتمک ہون اتے اکٹھے معلوم ہو سکن والے ہون۔

غیر-ساپیکھک کوانٹم مکینکس

سپیشل رلیٹیوٹی دے اثراں نوں لئے بگیر کناں دا کوانٹم مکینکس, اداہرن دے طور تے, پرکاش دی سپیڈ توں بہت گھٹ سپیڈاں اتے سنچارت ہو راے کناں دا کوانٹم مکینکس, غیر-ساپیکھک کوانٹم مکینکس کیہا جاندا جاندا اے۔ وکھریاں پرحالات لئی اس حوالہ وچ شروڈنگر اکیوئیشن دیاں کئی قسماں اگے لکھیاں ہن: سماں-آزاد اتے سماں-انحصار, اک اتے تن سپیشیئل ایام, اتے اک اتے $N$ کن۔

اصلی وچ, سسٹم رچن والے کن تھیوری وچ سنکھئک نام نہیں رکھدے۔ گنت دی بولی سانوں کناں دی پوزیشن دا اک جاں دوجے طریقے نال نامکرن کرن لئی مجبور کردی اے, نہیں تاں کہڑے کن واسطے کہڑے استھرانک پرسعنصر کرن والے چنہ ہندے ہن, درمیان, گلتوہمی ہو سکدی اے۔^[۳۰]

وقت آزاد

جیکر ہیملٹونیئن وقت دا کوئی واضع فنکشن نہ ہووے, تاں مساوات سپیشیئل اتے ٹینپورل حصیاں وچ نکھیڑنیوگ ہندی اے۔ عامطور تے, ویو فنکشن ایہہ روپ لے لیندا اے:

\Psi ({\text{space coords}},t)=\psi ({\text{space coords}})\tau (t)\,.

جتھے $ψ (سپیس نردیشانک)$ صرف سسٹم نوں رچن والے کناں دے سارے سپیشیئل نردیشانکاں (کوآرڈینیٹاں) دا اک فنکشن ہندا اے, اتے $τ (t)$ صرف وقت دا ہی اک فنکشن ہندا اے۔ $&psi؛$ نوں شروڈنگر اکیوئیشن وچ متعلق ایاماں دی آبادی وچ کناں دی متعلق آبادی لئی بھردے ہوئے, استھرانکاں دے نکھیڑ راہیں حل کرن توں مطلب اے سماں-انحصار مساوات دا عامَ حل ایہہ قسم دا ہندا ہندا اے:^[۱۵]

\Psi ({\text{space coords}},t)=\psi ({\text{space coords}})e^{-i{Et/\hbar }}\,.

کیونکہ سماں-انحصار فیز پھیکٹر ہمیشاں ہی اوہی رہندا اے, اسلئی صرف سپیشیئل حصیاں نوں ہی سماں-آزاد سمسیاواں لئی حل کرن دی لوڑ پیندی اے۔ اسدے نال ہی, توانائی اوپریٹر $' = iħ \partial / \partial t$ ہمیشاں ہی توانائی آئیگن-ملّ $E$ ولوں بدل دتے جانے چاہیدے ہن, جس کارن سماں-آزاد شروڈنگر اکیوئیشن ہیملٹونیئن اوپریٹر لئی اک آئیگن-ملّ اکیوئیشن ہندی اے:^[۵]^:143ff

{\hat {H}}\psi =E\psi

ایہہ کسے گنتی دے ایاماں (کسے سماں-آزاد پٹینشل وچ) وچ کسے گنتی دے کناں لئی سچ اے۔ ایہہ معاملہ سماں-انحصار اکیوئیشن دے سٹینڈنگ ترنگ ہلاں نوں درساؤندا اے, جو (وکھریاں اورجاواں دی کسے پروبیبلٹی وستھار-ونڈ دی بجائے) مقررہ توانائی والیاں حالتاں ہندیاں ہن۔ فزکس وچ, ایہناں سٹینڈنگ ترنگاں نوں سٹیشنری حالتواں جاں توانائی آئیگن-حالتواں کیہا جاندا اے؛ کیمیا وگیاب وچ ایہناں نوں ایٹومک اؤربٹل جاں مولیکیولر اؤربٹل کیہا جاندا اے۔ توانائی آئیگن-حالتاں دیاں سپرپجیشناں ایہناں دیاں خاصیتاں نوں توانائی لیولاں درمیان ساپیکھک پھیزاں مطابق بدل دندیاں ہن۔

اس اکیوئیشن توں توانائی آئیگن-ملّ قیمتاں دا اک اجاری سپیکٹرم رچدے ہن, اسلئی گنتک طور تے, توانائی ضرور ہی کوانٹائز ہونی چاہیدی اے۔ ہور خاص طور تے, توانائی آئیگن-حالتاں اک بیسس رچدیاں ہن- کوئی وی ویو فنکشن اجاری توانائی حالتاں اپر کسے جوڑ دے طور تے جاں جاری توانائی حالتاں اپر کسے انٹگرل دے طور تے لکھیا جا سکدا اے, جاں ہور سرو عام طور تے, کسے ناپ اپر کسے انٹگرل دے طور تے لکھیا جا سکدا اے۔ ایہہ گنت وچ سپیکٹرل تھیورم ہندی اے, اتے کسے محدود حالت سپیس اندر, ایہہ صرف ہرمشن میٹرکس دے آئیگن-ویکٹراں دی سمپورنتا دی اک سٹیٹمینٹ ہندی اے۔

اک-ایامی اداہرن

اک ایام اندرلے کسے کن لئی, ہیملٹونیئن ایہہ ہندا اے:

{\hat {H}}={\frac {{\hat {p}}^{2}}{2m}}+V(x)\,,\quad {\hat {p}}=-i\hbar {\frac {d}{dx}}

اتے اسنوں سرو عام شروڈنگر اکیوئیشن وچ بھرن تے ایہہ ملدا اے:

-{\frac {\hbar ^{2}}{2m}}{\frac {d^{2}}{dx^{2}}}\psi (x)+V(x)\psi (x)=E\psi (x)

ایہہ اکو اک معاملہ ہی ہندا اے جس وچ شروڈنگر اکیوئیشن اک انشک ڈفرینشیئل اکیوئیشن ہون نالوں, اک عام ڈفرینشیئل اکیوئیشن ہندی اے۔ جنرل حل ہمیشاں ہی اس قسم دے ہندے ہن:

\Psi (x,t)=\psi (x)e^{-iEt/\hbar }\,.

اک ایام اندرلے $N$ کناں لئی, ہیملٹونیئن ایہہ ہندا اے:

{\hat {H}}=\sum _{n=1}^{N}{\frac {{\hat {p}}_{n}^{2}}{2m_{n}}}+V(x_{1},x_{2},\cdots x_{N})\,,\quad {\hat {p}}_{n}=-i\hbar {\frac {\partial }{\partial x_{n}}}

جتھے کن $n$ دی پوزیشن $x n$ ہندی اے۔ متعلق شروڈنگر اکیوئیشن ایہہ ہندی اے:

-{\frac {\hbar ^{2}}{2}}\sum _{n=1}^{N}{\frac {1}{m_{n}}}{\frac {\partial ^{2}}{\partial x_{n}^{2}}}\psi (x_{1},x_{2},\cdots x_{N})+V(x_{1},x_{2},\cdots x_{N})\psi (x_{1},x_{2},\cdots x_{N})=E\psi (x_{1},x_{2},\cdots x_{N})\,.

اسلئی عامَ حل اس قسم دے ہندے ہن:

\Psi (x_{1},x_{2},\cdots x_{N},t)=e^{-iEt/\hbar }\psi (x_{1},x_{2}\cdots x_{N})

غیر-پرسپر کریاواں کردے نکھیڑنیوگ کناں لئی,^[۳۳] سسٹم دا پٹینشل صرف ہریک کن نوں وکھرے طور تے متاثر کردا اے, اسلئی کل پٹینشل توانائی ہریک کن لئی پٹینشل اورجاواں دا جوڑ ہندی اے:

V(x_{1},x_{2},\cdots x_{N})=\sum _{n=1}^{N}V(x_{n})\,.

اتے ویو فنکشن نوں ہریک کن لئی ویو فنکشناں دے کسے گننپھل دے روپ وچ لکھیا جا سکدا اے:

\Psi (x_{1},x_{2},\cdots x_{N},t)=e^{-i{Et/\hbar }}\prod _{n=1}^{N}\psi (x_{n})\,,

غیر-پرسپر کریاواں کردے اکو جاے کناں لئی, پٹینشل, اجے وی اک جوڑ ہی رہندا اے, پر ویو فنکشن ذرا ہور زیادہ گنجھل دار ہندا ہے- ایہہ کن وٹاندرے لئی جمیوار ہندا ہویا, وکھرے ویو فنکشناں دے گننپھل دیاں پرمیوٹیشناں اپر اک جوڑ ہو جاندا اے۔ عامطور وچ, پرسپر کریاواں کردے کناں لئی, اپروکت ویوجن ممکن نہیں ہندے۔

آزاد کن

زیرو پٹینشل لئی, $V = 0$ ہندا اے, اسلئی کن آزاد ہندا اے اتے اکیوئیشن انجھ پڑدی اے:^[۵]^:151ff

-E\psi ={\frac {\hbar ^{2}}{2m}}{d^{2}\psi  \over dx^{2}}\,

جو $E > 0$ ( $C n$ منچااے ستھرانک ہندے ہن) لئی ڈولدے (اؤسیلیٹ کردے) ہلاں والی ہندی اے:

\psi _{E}(x)=C_{1}e^{i{\sqrt {2mE/\hbar ^{2}}}\,x}+C_{2}e^{-i{\sqrt {2mE/\hbar ^{2}}}\,x}\,

اتے $E < 0$ لئی ایکپونینشیئل حل,

\psi _{-|E|}(x)=C_{1}e^{{\sqrt {2m|E|/\hbar ^{2}}}\,x}+C_{2}e^{-{\sqrt {2m|E|/\hbar ^{2}}}\,x}.\,

ایکپونینشیئل طور تے ودھ راے حل اک اننت نورم رکھدے ہن, اتے بھوتکی نہیں ہندے۔ ایہہ پیریؤڈک جاں پھکس کیتیاں ہوئیاں سیماواں دیاں شرطاں والے کسے محدود حجم وچ پروانت نہیں ہندے۔

آزاد کن اتے ہور زیادہ چرچہ لئی آزاد کن اتے ویوپیکٹ دیکھو۔

ستھر پٹینشل

کسے بیریئر اتے سٹی کسے ڈی بروگلِ ترنگ دی اینیمیشن

کسے ستھر پٹینشل لئی,

$V = V 0$ ہندا اے,
$E > V 0$ لئی, حل, اؤسیلیٹری ہدے ہن, اتے
$E < V 0$ لئی ایکپونینشیئل ہندے ہن,

جو اوہناں اورجاواں نال متعلق ہندے ہن جو کلاسیکل مکینکس وچ پروانت جاں اپروانت ہندیاں ہن۔ اؤسیلیٹری حل اک کلاسیکل طور تے پروانت توانائی والے ہندے ہن اتے اصلی کلاسیکل گتیاں نال سبدھّ رکھدے ہن, جدونکھ, ایکپونینشیئل حل اک اپروانت توانائی والے ہندے ہن اتے کوانٹم ٹنلنگ صدقہ, کلاسیکل طور تے اپروانت کھیتر وچ, کوانٹم بلیڈنگ دی اک چھوٹی مقدار نوں درساؤندے ہن۔ جیکر پٹینشل $V 0$ اننت تک ودھ جاندا اے, تاں رفتار کلاسیکل طور تے کسے محدود کھیتر تک محدود ہو جاندی اے۔ بہت دور توں دیکھن تے, ہریک حل کسے ایکپونینشیئل تک گھٹ جاندا اے؛ حالت کہ ایکپونینشیئل گھٹدا جاندا اے, توانائی لیولاں نوں کسے اجاری سیٹ تک روک دندی اے, جہناں نوں پروانت اورجاواں کیہا جاندا اے۔^[۳۱]

ہارمونک اؤسیلیٹر

اس پرحالت لئی شروڈنگر اکیوئیشن ایہہ ہندی اے؛

E\psi =-{\frac {\hbar ^{2}}{2m}}{\frac {d^{2}}{dx^{2}}}\psi +{\frac {1}{2}}m\omega ^{2}x^{2}\psi

حل کرن لئی ایہہ اک دھیان یوگ کوانٹم سسٹم ہندا اے؛ کیونکہ حل صحیح (پر گنجھلدار- ہرمائیٹ پولینومیئلاں دی بولی وچ) ہندے ہن, اتے ایہہ کمپن کر راے ایٹماں, انوآں سمیت, ہور سسٹماں دی اک وڈا ویرائٹی نوں درسا سکدا اے جاں گھٹو-گھٹو مختصر کر سکدا اے^[۳۴] اتے لیٹساں وچ ایٹماں جاں آئناں نوں,^[۳۵] اتے سنتلن نقطےآں نزدیک ہور پٹینشلاں نوں مختصر کر سکدا اے۔ ایہہ کوانٹم مکینکس وچ پرچربیشن طریقیاں دا ادھار وی ہندا اے۔ ہلاں دی اک پھیملی ہی ہندی ہے- پوزیشن بیسس وچ ایہہ حل ایہہ ہندے ہن؛

\psi _{n}(x)={\sqrt {\frac {1}{2^{n}\,n!}}}\cdot \left({\frac {m\omega }{\pi \hbar }}\right)^{1/4}\cdot e^{-{\frac {m\omega x^{2}}{2\hbar }}}\cdot H_{n}\left({\sqrt {\frac {m\omega }{\hbar }}}x\right)

جتھے

$n = 0,1,2,۔.۔$ اے, اتے
فنکشن $H n$ ہرمائیٹ پولینومیئل ہندے ہن۔

تنّ-ایامی اداہرناں

اک ایام توں تنّ-ایاماں تک دا پھلار سدھا ہی ہو جاندا اے, سارے پوزیشن اتے مومینٹم اوپریٹر اوہناں دیاں تنّ-ایامی سمیکرناں راہیں بدل دتیاں جاندیاں ہن اتے سپیس دے حوالہ وچ پارشل ڈیریویٹو گریڈیئنٹ اوپریٹر راہیں بدل دتا جاندا اے۔

تنّ-ایاماں وچ اک کن لئی ہیملٹونیئن ایہہ ہندا اے:

{\hat {H}}={\frac {{\hat {\mathbf {p} }}\cdot {\hat {\mathbf {p} }}}{2m}}+V(\mathbf {r} )\,,\quad {\hat {\mathbf {p} }}=-i\hbar \nabla

جو ایہہ اکیوئیشن پیدا کردا اے:

-{\frac {\hbar ^{2}}{2m}}\nabla ^{2}\psi (\mathbf {r} )+V(\mathbf {r} )\psi (\mathbf {r} )=E\psi (\mathbf {r} )

جو اس قسم دے سٹیشنری حالت ہلاں والی ہندی اے:

\Psi (\mathbf {r} ,t)=\psi (\mathbf {r} )e^{-iEt/\hbar }

جتھے کن دی پوزیشن $r$ ہندی اے۔ شروڈنگر اکیوئیشن حل کرن لئی دو لابھکاری “کو-آرڈینیٹ سسٹم” ایہہ ہن؛

کارٹیزیئن نردیشانک جہناں وچ $r = (x, y, z)$ رہندا اے, اتے
سپھیریکل پولر نردیشانکا, جہناں وچ $r = (r, θ, φ)$ ہندا اے۔

بے شکّ, ہور اؤرتھوگنل نردیشانک کجھ جیؤمیٹرک سمروپتاواں والے سسٹماں لئی اکیوئیشن نوں حل کرن لئی لابھکاری رہندے ہن۔ تن ایاماں اندر, $N$ کناں لئی, ہیملٹونیئن ایہہ ہندا اے:

{\hat {H}}=\sum _{n=1}^{N}{\frac {{\hat {\mathbf {p} }}_{n}\cdot {\hat {\mathbf {p} }}_{n}}{2m_{n}}}+V(\mathbf {r} _{1},\mathbf {r} _{2},\cdots \mathbf {r} _{N})\,,\quad {\hat {\mathbf {p} }}_{n}=-i\hbar \nabla _{n}

جتھے؛

کن $n$ دی پوزیشن $r n$ ہندی اے, اتے
گریڈیئنٹ اوپریٹر کن دی پوزیشن دے نردیشانکاں (کوآرڈینیٹاں) پرتِ حوالہ وچ پارشل ڈیریوٹو ہندے ہن۔

کارٹیزیئن نردیشانکاں (کوآرڈینیٹاں) اندر, کن $n$ لئی, پوزیشن ویکٹر $r n = (x n, y n, z n)$ ہندا اے۔ جدونکھ, گریڈیئنٹ اتے لیپلاسیئن اوپریٹر ترتیب وار ایہہ ہندے ہن:

\nabla _{n}=\mathbf {e} _{x}{\frac {\partial }{\partial x_{n}}}+\mathbf {e} _{y}{\frac {\partial }{\partial y_{n}}}+\mathbf {e} _{z}{\frac {\partial }{\partial z_{n}}}\,,\quad \nabla _{n}^{2}=\nabla _{n}\cdot \nabla _{n}={\frac {\partial ^{2}}{{\partial x_{n}}^{2}}}+{\frac {\partial ^{2}}{{\partial y_{n}}^{2}}}+{\frac {\partial ^{2}}{{\partial z_{n}}^{2}}}

شروڈنگر اکیوئیشن ایہہ ہندی اے:

-{\frac {\hbar ^{2}}{2}}\sum _{n=1}^{N}{\frac {1}{m_{n}}}\nabla _{n}^{2}\Psi (\mathbf {r} _{1},\mathbf {r} _{2},\cdots \mathbf {r} _{N})+V(\mathbf {r} _{1},\mathbf {r} _{2},\cdots \mathbf {r} _{N})\Psi (\mathbf {r} _{1},\mathbf {r} _{2},\cdots \mathbf {r} _{N})=E\Psi (\mathbf {r} _{1},\mathbf {r} _{2},\cdots \mathbf {r} _{N})

جو ایہناں سٹیشنری حالت ہلاں والی ہندی اے:

\Psi (\mathbf {r} _{1},\mathbf {r} _{2}\cdots \mathbf {r} _{N},t)=e^{-iEt/\hbar }\psi (\mathbf {r} _{1},\mathbf {r} _{2}\cdots \mathbf {r} _{N})

پھیر توں, غیر-پرسپر کریاواں کردے نکھیڑنیوگ کناں لئی, پٹینشل, کن پٹینشلاں دا جوڑ ہندا اے؛

V(\mathbf {r} _{1},\mathbf {r} _{2},\cdots \mathbf {r} _{N})=\sum _{n=1}^{N}V(\mathbf {r} _{n})

اتے ویو فنکشن کن ویو فنکشناں دا اک گننپھل ہندا اے؛

\Psi (\mathbf {r} _{1},\mathbf {r} _{2}\cdots \mathbf {r} _{N},t)=e^{-i{Et/\hbar }}\prod _{n=1}^{N}\psi (\mathbf {r} _{n})\,.

غیر-پرسپر کریاواں کردے اکو جاے کناں لئی, پٹینشل, اک جوڑ ہندا اے, پر ویو فنکشن, گننپھلاں دیاں پرمیوٹیشناں اپر اک جوڑ ہندا اے۔ پچھلیاں دو سمیکرناں پرسپر کریاواں کردے کناں تے لاگوُ نہیں ہندیاں ہن۔

اگے, اوہ اداہرناں ہن جتھے صحیح حل معلوم ہندے ہن۔ ہور وورناں لئی مکھ لیکھاں نوں دیکھو۔

ہائیڈروجن ایٹم

شروڈنگر اکیوئیشن دی اس قسم نوں ہائیڈروجن ایٹم تے لاگوُ کیتا جا سکدا اے:^[۲۶]^[۲۸]

E\psi =-{\frac {\hbar ^{2}}{2\mu }}\nabla ^{2}\psi -{\frac {e^{2}}{4\pi \varepsilon _{0}r}}\psi

جتھے؛

$e$ الیکٹرون چارج ہندا اے,
$r$ الیکٹرون دی پوزیشن ہندی اے ( $r = | r |$ پوزیشن دا خالص ملّ ہندا اے),
پٹینشل رقم کولومب پرسپر کریا کارن ہندی اے, جتھے کہ
$ε 0$ الیکٹرک ستھرانک (آزاد سپیس دی پرمٹیوٹی) ہندا اے اتے
$\mu ={\frac {m_{e}m_{p}}{m_{e}+m_{p}}}$ , پنج $m p$ والے ہائیڈروجن نیوکلیئس (صرف اک پروٹون) اتے $m e$ پنج والے اک الیکٹرون دا 2-باڈی گھٹیا ہویا پنج ہندا اے۔ نیگٹو چنہ پٹینشل رقم وچ آ جاندا اے کیونکہ پروٹون اتے الیکٹرون الٹ چارج والے ہندے ہن۔ الیکٹرون پنج دی جگہ گھٹیا ہویا پنج ورتیا جاندا اے کیونکہ الیکٹرون اتے پروٹون اکٹھیاں, اک سانجھے پنج دے مرکز دوالے اک دوجے نال چکر لگاؤندے ہن, اتے حل کرن لئی اک ٹو-باڈی مسئلہ رچدے ہن۔ الیکٹرون دی رفتار اتھے دلچسپی دا مکھ مرکز اے, اسلئی سامان اک-باڈی مسئلہ گھٹے ہوئے پنج نوں ورت کے الیکٹرون دی رفتار ہندی اے۔

ہائیڈروجن لئی ویو فنکشن الیکٹرون دے نردیشانکاں (کوآرڈینیٹاں) دا اک فنکشن ہندا اے, اتے اصلی وچ, ہریک نردیشانک دے فنکشناں وچ الگ کیتا جا سکدا اے۔^[۳۶] عامطور تے اسطراں سپھیریکل پولر نردیشانکاں وچ کیتا جاندا اے:

\psi (r,\theta ,\phi )=R(r)Y_{\ell }^{m}(\theta ,\phi )=R(r)\Theta (\theta )\Phi (\phi )

جتھے؛

$R$ ریڈیئل فنکشن کاے جاندے ہن اتے
$Y m ℓ (θ, φ)$ ڈگری $ℓ$ اتے اؤرڈر $m$ والے سپھیریکل ہارمونک ہندے ہن۔

ایہہ اکو اک اجیہا ایٹم ہندا اے جس لئی شروڈنگر اکیوئیشن صحیح طور تے حل کیتی گئی اے۔ ملٹی-الیکٹرون ایٹم سنکھیپیؤ ودھیاں منگدے ہن۔ ہلاں دی پھیملی ایہہ اے:^[۳۷]

\psi _{n\ell m}(r,\theta ,\phi )={\sqrt {{\left({\frac {2}{na_{0}}}\right)}^{3}{\frac {(n-\ell -1)!}{2n[(n+\ell )!]}}}}e^{-r/na_{0}}\left({\frac {2r}{na_{0}}}\right)^{\ell }L_{n-\ell -1}^{2\ell +1}\left({\frac {2r}{na_{0}}}\right)\cdot Y_{\ell }^{m}(\theta ,\phi )

جتھے:

$a_{0}={\frac {4\pi \varepsilon _{0}\hbar ^{2}}{m_{e}e^{2}}}$ بوہر دا ریڈیئس اے,
$L_{n-\ell -1}^{2\ell +1}(\cdots )$ ڈگری $n - ℓ - 1$ دے سرو عام کیتے ہوئے پولینومیئل ہندے ہن۔
$n, ℓ, m$ ترتیب وار, مکھ, ایزیمیوتھل, اتے چمبکی کوانٹم نمبر ہندے ہن: جو ایہہ ملّ لیندے ہن:

{\begin{aligned}n&=1,2,3,\dots \\\ell &=0,1,2,\dots ,n-1\\m&=-\ell ,\dots ,\ell \\\end{aligned}}

NB: سرو عام کیتے ہوئے پولینومیئل وکھرے ودواناں راہیں وکھرے طور تے متاثر کیتے گئے ہن- ایہناں اتے مکھ لیکھ دیکھو اتے ہائیڈوجن ایٹم دیکھو۔

دو-الیکٹرون ایٹم جاں آئن

کسے دو-الیکٹرون سسٹم لئی اکئیشن, جویں نیوٹرل ہیلیئم ایٹم (He, $Z = 2$ ), نیگٹو ہائیڈروجن آئن (H⁻, $Z = 1$ ), جاں پوزٹو لیتھیئم ائن (Li⁺, $Z = 3$ ) ایہہ ہندی اے:^[۲۹]

E\psi =-\hbar ^{2}\left[{\frac {1}{2\mu }}\left(\nabla _{1}^{2}+\nabla _{2}^{2}\right)+{\frac {1}{M}}\nabla _{1}\cdot \nabla _{2}\right]\psi +{\frac {e^{2}}{4\pi \varepsilon _{0}}}\left[{\frac {1}{r_{12}}}-Z\left({\frac {1}{r_{1}}}+{\frac {1}{r_{2}}}\right)\right]\psi

جتھے؛

$r 1$ الیکٹرون دی پوزیشن ہندی اے ( $r 1 = | r 1 |$ اسدا میگنیٹیوڈ ہدا اے),
$r 2$ دوجے الیکٹرون دی پوزیشن ہندی اے ( $r 2 = | r 2 |$ میگنیٹیوڈ ہندا اے),
$r 12 = | r 12 |$ ایہناں درمیان دوری دا میگنیٹیوڈ ہندا اے جو اس راہیں ملدا اے؛

|\mathbf {r} _{12}|=|\mathbf {r} _{2}-\mathbf {r} _{1}|\,\!

$μ$ , پھیر توں, پنج $M$ والے نیوکلیئس دے حوالہ وچ کسے الیکٹرون دا ٹو-باڈی گھٹیا ہویا پنج ہندا اے, اسلئی ٹائم

\mu ={\frac {m_{e}M}{m_{e}+M}}\,\!

اتے

$Z$ , تتّ لئی ایٹومک نمبر ہندا اے (کوانٹم نمبر نہیں ہندا)۔

دوویں لیپلاسیئناں دی کروس-رقم؛

{\frac {1}{M}}\nabla _{1}\cdot \nabla _{2}\,\!

نوں پنج پولرائزیشن رقم دے طور تے جانیا جاندا اے, جو ایٹومک نیوکلیائی دی رفتار کرکے پیدا ہندی اے۔ ویو فنکشن, دوویں الیکٹروناں دیاں پزیشناں دا اک فنکشن ہندا اے۔

\psi =\psi (\mathbf {r} _{1},\mathbf {r} _{2}).

اس اکیوئیشن لئی کوئی بند قسم دا حل نہیں ہندا۔

وقت انحصار

ایہہ کوانٹم حالت لئی رفتار دی مساوات ہدی اے۔ سبھ توں زیادہ سرو عام روپ وچ, اسنوں انجھ لکھیا جاندا اے:^[۵]^:143ff

i\hbar {\frac {\partial }{\partial t}}\Psi ={\hat {H}}\Psi .

اتے حل, ویو فنکشن, سسٹم اتے ٹائم دے سارے کن نردیشانکاں (کوآرڈینیٹاں) دا اک فنکشن ہندا اے۔ خاص معاملے اگے لکھے گئے ہن۔

اک ایام اندر اک کن لئی, ہیملٹونیئن؛

{\hat {H}}={\frac {{\hat {p}}^{2}}{2m}}+V(x,t)\,,\quad {\hat {p}}=-i\hbar {\frac {\partial }{\partial x}}

ایہہ اکیوئیشن پیدا کردا اے:

i\hbar {\frac {\partial }{\partial t}}\Psi (x,t)=-{\frac {\hbar ^{2}}{2m}}{\frac {\partial ^{2}}{\partial x^{2}}}\Psi (x,t)+V(x,t)\Psi (x,t)

اک ایام اندرلے $N$ کناں لئی, ہیملٹونیئن ایہہ ہندا اے:

{\hat {H}}=\sum _{n=1}^{N}{\frac {{\hat {p}}_{n}^{2}}{2m_{n}}}+V(x_{1},x_{2},\cdots x_{N},t)\,,\quad {\hat {p}}_{n}=-i\hbar {\frac {\partial }{\partial x_{n}}}

جتھے کن $n$ دی پوزیشن $x n$ ہندی اے, جو ایہہ اکیوئیشن پیدا کر رہی ہندی اے:

i\hbar {\frac {\partial }{\partial t}}\Psi (x_{1},x_{2}\cdots x_{N},t)=-{\frac {\hbar ^{2}}{2}}\sum _{n=1}^{N}{\frac {1}{m_{n}}}{\frac {\partial ^{2}}{\partial x_{n}^{2}}}\Psi (x_{1},x_{2}\cdots x_{N},t)+V(x_{1},x_{2}\cdots x_{N},t)\Psi (x_{1},x_{2}\cdots x_{N},t)\,.

تن ایاماں اندرلے اک کن لئی, ہیملٹونیئن ایہہ ہندا اے:

{\hat {H}}={\frac {{\hat {\mathbf {p} }}\cdot {\hat {\mathbf {p} }}}{2m}}+V(\mathbf {r} ,t)\,,\quad {\hat {\mathbf {p} }}=-i\hbar \nabla

جو ایہہ اکیوئیشن پیدا کردا اے:

i\hbar {\frac {\partial }{\partial t}}\Psi (\mathbf {r} ,t)=-{\frac {\hbar ^{2}}{2m}}\nabla ^{2}\Psi (\mathbf {r} ,t)+V(\mathbf {r} ,t)\Psi (\mathbf {r} ,t)

تنّ-ایاماں اندرلے $N$ کناں لئی, ہیملٹونیئن ایہہ ہندا اے:

{\hat {H}}=\sum _{n=1}^{N}{\frac {{\hat {\mathbf {p} }}_{n}\cdot {\hat {\mathbf {p} }}_{n}}{2m_{n}}}+V(\mathbf {r} _{1},\mathbf {r} _{2},\cdots \mathbf {r} _{N},t)\,,\quad {\hat {\mathbf {p} }}_{n}=-i\hbar \nabla _{n}

جتھے کن $n$ دی پوزیشن $r n$ ہندی اے, جو ایہہ اکیوئیشن پیدا کردی اے:^[۵]^:141

i\hbar {\frac {\partial }{\partial t}}\Psi (\mathbf {r} _{1},\mathbf {r} _{2},\cdots \mathbf {r} _{N},t)=-{\frac {\hbar ^{2}}{2}}\sum _{n=1}^{N}{\frac {1}{m_{n}}}\nabla _{n}^{2}\Psi (\mathbf {r} _{1},\mathbf {r} _{2},\cdots \mathbf {r} _{N},t)+V(\mathbf {r} _{1},\mathbf {r} _{2},\cdots \mathbf {r} _{N},t)\Psi (\mathbf {r} _{1},\mathbf {r} _{2},\cdots \mathbf {r} _{N},t)

ایہہ آخری اکیوئیشن اک بہت اچے ایام وچ ہندی اے, اسلئی اسدے حل دیکھنے اسان نہیں ہن۔

حل ودھیاں

عامَ تکنیکاں:

خاص ماملاں واسطے ودھیاں:

اینالٹیکل ہلاں والے کوانٹم-مکینیکل سسٹماں دی لسٹ
ہارٹی-پھوک تکنیک اتے پوسٹ ہارٹی-پھوک ودھیاں

خاصیتاں

شروڈنگر اکیوئیشن اگے لکھیاں خاصیتاں رکھدی اے: کجھ لابھکاری ہن, پر کمیاں بچدیاں ہن۔ انت نوں, ایہہ خاصیتاں ورتے جاندے ہیملٹونیئن توں پیدا ہندیاں ہن, اتے اکیوئیشن پرتِ ہلاں توں پیدا ہندیاں ہن۔

ریکھکتا

ہور دیکھو: لینیئر ڈفرینشیئل اکئیشن

اوپروکت ترقی اندر, شروڈنگر اکیوئیشن سرو سدھارنتا لئی ریکھک بنائی گئی سی, بھاویں اسدے ہور اثر پیندے ہن۔ جیکر دو ویو فنکشن $ψ 1$ اتے $ψ 2$ حل ہون, تاں پھیر ایہناں دوواں دا کوئی وی ریکھک میل وی اک حل ہی ہندا اے:

\displaystyle \psi =a\psi _{1}+b\psi _{2}

جتھے $a$ اتے $b$ کوئی وی کمپلیکس نمبر ہو سکدے ہن (جوڑپھل نوں ویو فنکشناں دی کسے وی گنتی تک ودھایا جا سکدا اے)۔ ایہہ خاصیت (خاصیت) کوانٹم حالتاں دیاں سپرپجیشناں نوں شروڈنگر اکیوئیشن دے حل ہون دی آگیا دندی اے۔ ہور وی سرو عام طور تے, ایہہ لاگوُ رہندا اے کہ شروڈنگر اکیوئیشن پرتِ سرو عام ہلاں نوں سارے سنگل حالت حاصل کیتے جان یوگ ہلاں اپر اک حاصل کیتے جوڑ نوں لین صدقہ کھوجیا جا سکدا اے۔ اداہرن دے طور تے, اک ویو فنکشن $Ψ (x, t)$ تے وچار کرو کہ ایہہ ویو فنکشن دو فنکشناں دا اک گننپھل راے: اک سماں-آزاد فنکشن, اتے اک سماں-انحصار فنکشن۔ جیکر سماں-آزاد شروڈنجر مساوات ورت کے کھوجیاں مقررہ توانائی دیاں حالتاں اینپلیٹیوڈ $A n$ والے $ψ E (x)$ نال دتیاں جاندیاں ہون, اتے سماں انحصار فیز پھیکٹر اس طرحاں دتا جاندا ہووے,

e^{{-iE_{n}t}/\hbar },

تاں اک مصدقہ سرو عام حل ایہہ ہندا اے؛

\displaystyle \Psi (x,t)=\sum \limits _{n}A_{n}\psi _{E_{n}}(x)e^{{-iE_{n}t}/\hbar }.

اسدے نال ہی, ہلاں نوں ناپن دی اہلیت کسے ویو فنکشن نوں پہلاں نورملائز کیتے بغیر ہی اسدے لئی حل دی آگیا دندی اے۔ جیکر نورملائز کیتے ہوئے ہلاں دا اک سیٹ $ψ n$ ہووے, تاں پھیر؛

\displaystyle \Psi =\sum \limits _{n}A_{n}\psi _{n}

نوں ایہہ یقینی بنا کے نورملائز کیتا جا سکدا اے؛

\displaystyle \sum \limits _{n}|A_{n}|^{2}=1

ایہہ اسنوں ثابت کرن نالوں کتے زیادہ سودھاجنک رہندا اے کہ؛

\displaystyle \int \limits _{-\infty }^{\infty }|\Psi (x)|^{2}\,dx=\int \limits _{-\infty }^{\infty }\Psi (x)\Psi ^{*}(x)\,dx=1.

اصلی ارجا آئیگن-حالتاں

سماں-آزاد اکیوئیشن لئی, ریکھکتا دا اک وادھو لچھن انجھ اے: جیکر دو ویو فنکشن $ψ 1$ اتے $&psi؛ 2$ , سماں-آزاد اکیوئیشن دے اوسے توانائی $E$ سمیت حل ہون, تاں ایہناں دا کوئی وی ریکھک میل وی اک حل ہی ہندا اے:

{\hat {H}}(a\psi _{1}+b\psi _{2})=a{\hat {H}}\psi _{1}+b{\hat {H}}\psi _{2}=E(a\psi _{1}+b\psi _{2}).

اکو توانائی والے دو وکھرے ہلاں نوں ڈیجنریٹ کیہا جاندا اے۔^[۳۱]

کسے منچااے پٹینشل اندر, جیکر کوئی ویو فنکشن $ψ$ سماں-آزاد اکیوئیشن نوں حل کردا اے, تاں اسدا کمپلیکس کنجوگیٹ, جو $ψ *$ نال درسایا جاندا اے, وی اجیہا ہی کردا اے۔ ریکھک میل لے کے, $ψ$ دے اصلی اتے خیالی حصے, دوویں ہی حل ہندے ہن۔ جیکر کوئی وی ڈیجنریسی نہ ہووے تاں ایہہ صرف اک پھیکٹر راہیں ہی انتر رکھدے ہندے ہن۔

سماں-انحصار اکیوئیشن اندر, کمپلیکس کنجوگیٹ ترنگاں الٹ سمتاں وچ رفتار کردیاں ہن۔ جیکر $Ψ (x, t)$ اک حل ہووے, تاں $Ψ *(x, - t)$ وی اک حل ہی ہندا اے۔ کمپلیکس کنجوگیشن دی سمروپیؤ نوں ٹائم-رورسل سمروپیؤ کیہا جاندا اے۔

سپیس اتے ٹائم ڈیریویٹو

سپیس وچ شروڈنگر اکیوئیشن دوجے اتے وقت وچ پہلے اؤرڈر دی اکیوئیشن ہندی اے, جو کسے کوانٹم حالت دی ویلے وچ اتپتی درساؤندی اے (یانِ کہ, ایہہ حال توں مستقبل دا اینپلیٹیوڈ مقرر کردی اے)۔

3-ایامی کارٹیزیئن نردیشانکاں (کوآرڈینیٹاں) اندر واضع طور تے اک کن لئی- اکیوئیشن ایہہ ہندی اے؛

i\hbar {\partial \Psi  \over \partial t}=-{\hbar ^{2} \over 2m}\left({\partial ^{2}\Psi  \over \partial x^{2}}+{\partial ^{2}\Psi  \over \partial y^{2}}+{\partial ^{2}\Psi  \over \partial z^{2}}\right)+V(x,y,z,t)\Psi .\,\!

پہلے ٹائم ڈیریویٹو توں مطلب اے ویو فنکشن دا ( $t = 0$ اتے) شروعاتی ملّ

\Psi (x,y,z,0)\,\!

کوئی منچاہا ستھرانک ہندا اے۔ اسیتراں- سپیس دے حوالہ وچ دوجے اؤرڈر دے ڈیریویٹواں توں مطلب اے ویو فنکشن اتے اسدے پہلے اؤرڈر دے سپیشیئل ڈیریویٹو

{\begin{aligned}&\Psi (x_{b},y_{b},z_{b},t)\\&{\frac {\partial }{\partial x}}\Psi (x_{b},y_{b},z_{b},t)\quad {\frac {\partial }{\partial y}}\Psi (x_{b},y_{b},z_{b},t)\quad {\frac {\partial }{\partial z}}\Psi (x_{b},y_{b},z_{b},t)\end{aligned}}\,\!

سارے ہی نقطےآں دے کسے دتے ہوئے سیٹ اتے منچااے ستھرانک ہندے ہن, جتھے $x b$ , $y b$ , $z b$ اجیاے نقطےآں دا اک سیٹ ہندے ہن جو سیما $b$ نوں درسا راے ہندے ہن (ڈیریویٹو حداں اتے لئے جاندے ہن)۔ کھاستور تے, اک جاں دو حداں ہندیاں ہن, جویں ترتیب وار, سٹیپّ پٹینشل اتے کسے بوکس وچ کن۔

جویں پہلے اؤرڈر والے ڈیریویٹو منچااے ہندے ہن, اسیتراں ویو فنکشن وی سپیس دا اک جاری طور تے ڈپھرینشیئیبل فنکشن ہندا اے کیونکہ کسے وی سیما اتے, ویو فنکشن دا گریڈیئنٹ میچ کیتا جا سکدا اے۔

استوں الٹ, فزکس وچ ویو فنکشن عامطور تے وقت وچ دوجے اؤرڈر والے ہندے ہن, کلاسیکل ویو اکئیشناں اتے کوانٹم کلیئن-جورڈن اکویئیشن نوٹ کرن یوگ ہن۔

پروبیبلٹی دی مقامی سرکھئتا

شروڈنگر اکیوئیشن پروبیبلٹی کنزرویشن دے مطابق ہندی اے۔ شروڈنگر اکیوئیشن دے سجے پاسے کمپلیکس کنجوگیٹ ویو فنکشن نال گننپھل کرن تے, اتے ویو فنکشن دے کھبے پاسے شروڈنگر اکیوئیشن دے کمپلیکس کنجوگیٹ نال گننپھل کرن تے, اتے پھیر دوواں دا گھٹاؤ کرن تے, پروبیبلٹی لئی نرنترتا مساوات ملدی اے:^[۳۸]

{\partial  \over \partial t}\rho \left(\mathbf {r} ,t\right)+\nabla \cdot \mathbf {j} =0,

جتھے؛

\rho =|\Psi |^{2}=\Psi ^{*}(\mathbf {r} ,t)\Psi (\mathbf {r} ,t)\,\!

پروبیبلٹی کثافت (پروبیبلٹی پرتِ یونٹ وولیؤم, , $*$ کمپلیکس کنجوگیٹ نوں درساؤندا اے) ہندی اے, اتے

\mathbf {j} ={1 \over 2m}\left(\Psi ^{*}{\hat {\mathbf {p} }}\Psi -\Psi {\hat {\mathbf {p} }}\Psi ^{*}\right)\,\!

پروبیبلٹی کرنٹ (جو پرتِ یونٹ کھیترپھل وہندا اے) ہندا اے۔

اسطراں شروڈنگر اکیوئیشن توں اندازا, پروبیبلٹی سرکھئتا دی النگھنا نہیں کردے۔

پوزٹو اینرجی

جیکر پٹینشل ہیٹھاں توں بنیا ہویا ہووے, یانِ کہ, پٹینشل توانائی دی کوئی نیونتم قیمت ہندی ہووے, تاں شروڈنگر اکیوئیشن دے آئیگن-فنکشن اجیہی توانائی والے ہندے ہن جو تھلے توں بنی ہندی اے۔ اس نوں ہیٹھاں لکھے مطابق, ویریئیشنل پرنسپل ورتدے ہوئے سبھ توں زیادہ اسانی نال دیکھیا جا سکدا اے۔ (تھلے وی دیکھو) تھلے توں بنے ہوئے کسے وی لینیئر اوپریٹر $'$ لئی, گھٹ توں گھٹ آئیگن-ملّ والا آئیگن-ویکٹر, ویکٹر $ψ$ ہندا اے جو اس مقدار نوں سارے $ψ$ اتے منیمائیز (گھٹ توں گھٹ) کردا اے:

\langle \psi |{\hat {A}}|\psi \rangle

جو مانکیکرت ہندے ہن۔^[۳۸] اسطراں, نیونتم آئیگن-ملّ نوں ویریئیشنل اصول راہیں لکھیا جاندا اے۔ تھلے توں باؤنڈ کیتے (بنے ہوئے) شروڈنجر ہیملٹونیئن $Ĥ$ لئی, نیونتم آئیگن-ملّ نوں ادھار حالت توانائی کیہا جاندا اے۔ اوہ توانائی؛

\langle \psi |{\hat {H}}|\psi \rangle =\int \psi ^{*}(\mathbf {r} )\left[-{\frac {\hbar ^{2}}{2m}}\nabla ^{2}\psi (\mathbf {r} )+V(\mathbf {r} )\psi (\mathbf {r} )\right]d^{3}\mathbf {r} =\int \left[{\frac {\hbar ^{2}}{2m}}|\nabla \psi |^{2}+V(\mathbf {r} )|\psi |^{2}\right]d^{3}\mathbf {r} =\langle {\hat {H}}\rangle

دا نیونتم ملّ ہندا اے (حصیاں راہیں انٹیگریشن ورتدے ہوئے)۔ $ψ 2$ دے کمپلیکس موڈولس (جو مقررہ طور تے پوزٹو ہندا اے) صدقہ, سجا پاسہ ہمیشاں ہی $V (x)$ دے نیونتم ملّ توں زیادہ رہندا اے۔ خاص طور وچ, گراؤنڈ سٹیٹ اینرجی اودوں پوزٹو رہندی اے جدوں $V (x)$ سبھ جگہ پوزٹو ہووے۔

جہڑے پٹینشل تھلے توں بنے ہندے ہن اتے کسے کھیتر اپر اننت نہیں ہندے, اوہناں لئی, اک اجیہی ادھار حالت ہندی اے جو انٹگرل نوں اپر توں منیمائیز کردی اے۔ ایہہ نیونتم توانائی ویو فنکشن اصلی اتے مقررہ طور تے پوزٹو ہندا ہے- جسدا مطلب اے کہ ویو فنکشن ودھ اتے گھٹ سکدا اے, پر ساریاں پوزیشناں لئی پوزٹو ہی رہندا اے۔ ایہہ بھوتکی طور تے نیگٹو نہیں ہو سکدا: جیکر اجیہا ہندا, تاں چنہ تبدیلی ویلے موڑاں نوں (ویو فنکشن نوں منیمائیز کرن لئی) سچارو کرن نال تیزی نال انٹگرل پرتِ گریڈیئنٹ یوگدان گھٹ جاندا اتے اسے کارن کائنیٹک اینرجی وی گھٹ جاندی, جدونکھ پٹینشل توانائی ریکھک طور تے اتے گھٹ تیزی نال بدلدی۔ کائینیٹک اتے ستھتک توانائی دوویں ہی وکھریاں دراں نال تبدیل ہندیاں, تاں جو کل توانائی ستھر نہ رہندی, جو واپر نہیں سکدا (سرکھئتا)۔ حل, شروڈنگر اکیوئیشن نال تاں مطابق رہندے ہن جیکر ایہہ ویو فنکشن مقررہ طور تے پوزٹو رہندا ہووے۔

چنہ تبدیلیاں دی کمی ایہہ وی ثابت کردی اے کہ ادھار حالت غیر-ڈجنریٹ ہندی اے, کیونکہ جیکر سانجھی توانائی $E$ والیاں دو ادھار حالتاں ہندیاں, جو اک-دوجی دے انوپاتی نہ ہندیاں ہون, تاں دوواں دا اک اجیہا ریکھک میل وی ہونا چاہیدا اے جو کسے زیرو حل وچ نتیجہ دین والی اک ادھار حالت وی ہندا۔

ڈفیوزن پرتِ وشلیشناتمک نرنترتا

ہور دیکھو: پاتھ انٹگرل فارمولا ویونتبندی#شروڈنگر اکیوئیشن

اوپروکت خاصیت (توانائی دی پوزٹو نشچتتا) شروڈنگر اکیوئیشن دے کوئی سٹوکاسٹک پروسیسّ ہون دی وشلیشناتمک نرنترتا نوں آگیا دندی اے۔ اسدی وضاحت ڈی بروگلِ ترنگاں پرتِ لاگوُ کیتے جان والے ہوئیجینس-پھریسنل اصول دے طور تے کیتی جا سکدی اے؛ پھیل راے ویوفرنٹ, گھلمل راے پروبیبلٹی اینپلیٹیوڈ ہندے ہن۔^[۳۸]

کوئی منچاہی سیر کر راے کسے آزاد کن (جو کسے پٹینشل دا ساہمنا نہیں کر رہا ہندا) لئی, سماں-انحصار شروڈنگر اکیوئیشن وچ $τ = it$ بھردے ہوئے, ایہہ حاصل ہندا اے:^[۳۹]

{\partial  \over \partial \tau }X(\mathbf {r} ,\tau )={\frac {\hbar }{2m}}\nabla ^{2}X(\mathbf {r} ,\tau )\,,\quad X(\mathbf {r} ,\tau )=\Psi (\mathbf {r} ,\tau /i)

جو ڈفیوزن اکویئیشن دی قسم ورگی قسم دا ہی ہندا اے, جسدے ڈفیوزن گنانک $ħ / 2 m$ ہندے ہن۔ اوس معاملے وچ, گھلملتا (ڈپھیوزیوٹی), مارکوو پروسیسّ مطابق ڈی بروگلی تعلق پیدا کردی اے۔ ^[۴۰]

نیمتتا

سکئیئر-انٹیگریبل ڈینسٹیاں دی سپیس $L^{2}$ اتے, شروڈنجر اردھ-گروہ (سیمی-گروپ) $e^{it{\hat {H}}}$ , اک یونائٹری اوتپتی ہندی اے, اتے اسے لئی ایہہ وشاتمک ہندی اے۔ پرواہ, شروڈنگر اکیوئیشن $i\partial _{t}u={\widehat {H}}u$ دی پالنا کردے ہن, جتھے ڈیریویٹو نوں وستھار-ونڈ مطلب وچ لیا جاندا اے۔ پھیر وی, کیونکہ سبھ توں زیادہ ڈھکویں ہیملٹونیئناں (جویں, کسے پٹینشل راہیں ممکن طور تے سودھیا ہویا لیپلیس اوپریٹر) لئی ${\widehat {H}}$ , $L^{2}$ , اندر بنیا نہیں ہندا, ایہہ ثابت کردا اے کہ اردھ-گروہ پرواہ عامطور وچ سوبوللیو نیمتتا دی کمی والے ہندے ہن۔ اسدی جگہ, شروڈنگر اکیوئیشن دے حل کسے سٹرچارٹز اندازا تے کھرے اتردے ہن۔

ساپیکھک کوانٹم مکینکس

ساپیکھک (ریلیٹیوسٹک) کوانٹم مکینکس اتھے حاصل کیتا جاندا اے, جتھے کوانٹم مکینکس اتے سپیشل رلیٹیوٹی اکٹھے لاگوُ ہندے ہون۔ عامطور وچ, کلاسیکل توانائی اکئیشناں دی بجائے, ساپیکھک (ریلیٹیوسٹک) اورجا-مومینٹم تعلق توں ساپیکھک (ریلیٹیوسٹک) ویو اکئیشناں بناؤنیاں پسند کیتیاں جاندیاں ہن۔

E^{2}=(pc)^{2}+(m_{0}c^{2})^{2}\,,

کلیئن-جورڈن اکویئیشن اتے ڈیراک اکویئیشن دو اجہیاں سمیکرناں ہن۔ کلیئن-گورڈن اکئیشن,

{\frac {1}{c^{2}}}{\frac {\partial ^{2}}{\partial t^{2}}}\psi -\nabla ^{2}\psi +{\frac {m^{2}c^{2}}{\hbar ^{2}}}\psi =0.

,

حاصل کیتی جان والی اجیہی پہلی مساوات سی۔, جو غیر-ساپیکھک (نون-ریلیٹیوسٹک) اکیوئیشن توں وی پہلاں حاصل کر لئی گئی سی, اتے ایہہ پنج-یکت سپنّ-ہین کناں تے لاگوُ ہندی اے۔ ڈیراک اکئیشن, دو اجیاے اوپریٹراں دے کسے گننپھل وچ سارے دے سارے ساپیکھک (ریلیٹیوسٹک) ویو اوپریٹر نوں پھیکٹرائز کرن نال کلیئن-گورڈن اکیوئیشن دا طبقہ مول لیندے ہوئے, پیدا ہندی ہے- جہناں وچوں اک اوپریٹر ساری دی ساری ڈیراک اکیوئیشن لئی اوپریٹر ہندا اے۔

رلیٹیوٹی وچ شروڈنگر اکیوئیشن دی سرو عام قسم سچ رہندی اے, پر ہیملٹونیئن دی سپشٹتا گھٹ جاندی اے۔ اداہرن دے طور تے, کسے پنج $m$ اتے الیکٹرک چارج $q$ والے کسے کن لئی, کسے الیکٹرومیگنیٹک فیلڈ (الیکٹرومیگنٹزم پٹینشلاں $φ$ اتے $A$ راہیں درسائی جاندی) اندر, ڈیراک ہیملٹونیئن ایہہ ہندا اے:

{\hat {H}}_{\text{Dirac}}=\gamma ^{0}\left[c{\boldsymbol {\gamma }}\cdot \left({\hat {\mathbf {p} }}-q\mathbf {A} \right)+mc^{2}+\gamma ^{0}q\phi \right]\,,

جس وچ, $γ = (γ 1, γ 2, γ 3)$ اتے $γ 0$ , کن دے سپنّ نال متعلق ڈیراک گاما میٹرکس ہندے ہن۔ ڈیراک اکیوئیشن سارے سپنّ-¹⁄₂ کناں لئی سچ رہندی اے, اتے اکیوئیشن پرتِ حل, 4-کمپونینٹ سپنور فیلڈاں ہندیاں ہن, جہناں دے دو کمپونینٹ کن نال تعلق رکھن والے ہندے ہن اتے باقی دے دو کمپونینٹ اینٹی-پارٹیکل نال متعلق ہندے ہن۔

کلیئن-گورڈن اکیوئیشن لئی, شروڈنگر اکیوئیشن دی سرو عام قسم ورتنی سودھاجنک رہندی اے, اتے مشق وچ, ہیملٹونیئن ڈیراک ہیملٹونیئن پرتِ کسے تلّ طریقے وچ سمیکرنبدھّ نہیں کیتا جاندا۔ ساپیکھک (ریلیٹیوسٹک) کوانٹم پھیلڈاں واسطے سمیکرناں نوں ہور طریقیاں نال حاصل کیتا جا سکدا اے, جویں کسے لگرانجیئن کثافت توں شروع کرکے اتے پھیلڈاں لئی الر-لگرانج اکئیشناں ورتدے ہوئے, جاں لورنٹز گروپ دی پرستتی تھیوری ورت کے, جس وچ کجھ پرستتیاں نوں دتے ہوئے سپنّ (اتے پنج) والے کسے آزاد کن لئی اکیوئیشن نوں حل کرن لئی ورتیا جا سکدا اے۔

عامطور وچ, سرو عام شروڈنگر اکیوئیشن وچ بھریا جان والا ہیملٹونیئن صرف پوزیشن اتے مومینٹم اوپریٹراں (اتے ممکن طور تے ویلے) دا ہی اک فنکشن نہیں ہندا, سگوں سپنّ میٹرکساں دا وی اک فنکشن ہندا اے۔ اسدے نال ہی, $s$ سپنّ والے, کسے پنج-یکت کن لئی, کسے ساپیکھک (ریلیٹیوسٹک) ترنگ مساوات پرتِ حل, کمپلیکس ملاں والیاں $2(2 s + 1)$ -کمپونینٹ سپنور فیلڈاں ہندیاں ہن۔

کوانٹم فیلڈ تھیوری

سرو عام (شروڈنجر) اکیوئیشن کوانٹم فیلڈ تھیوری وچ وی ورتی جاندی اے, اتے مصدقہ رہندی اے, جو ساپیکھک (ریلیٹیوسٹک) اتے غیر-ساپیکھک (غیر-ریلیٹیوسٹک) دوویں قسم دے ہلاں لئی اجیہا ہندی اے۔ پھیر وی, حل $ψ$ کسے ترنگ دے طور تے ویاکھئت نہیں کیتا جاندا, سگوں کسے پھوک سپیس اندر موجود حالتاں اتے کریا کرن والے کسے اوپریٹر دے طور تے ویاکھئت ہونا چاہیدا اے۔^{[حوالہ درکار]}

پہلی گھات والی قسم

شروڈنگر اکیوئیشن نوں اوسے انداز وچ اک پہلے درجے^[۴۱]^[۴۲]^[۴۳] دی قسم توں وی ویونتبند کیتا جا سکدا اے, جس وچ کلیئن-جورڈن اکویئیشن نوں ڈیراک اکویئیشن توں ویونتبند کیتا جا سکدا اے۔ 1 D وچ پہلے درجے دی اکیوئیشن ایہہ ہندی اے؛

{\begin{aligned}-i\partial _{z}\psi =(i\eta \partial _{t}+\eta ^{\dagger }m)\psi \end{aligned}}

ایہہ اکیوئیشن غیر-ساپیکھک کوانٹم مکینکس اندر سپنّ نوں شامل کرن دی آگیا دندی اے۔ اپروکت اکیوئیشن دا طبقہ کرن نال 1 D وچ شروڈنگر اکیوئیشن حاصل ہندی اے۔ میٹرکس $\eta$ اگے لکھیاں خاصیتاں دا پالن کردے ہن؛

{\begin{aligned}\eta ^{2}=0\\(\eta ^{\dagger })^{2}=0\\\left\lbrace \eta ,\eta ^{\dagger }\right\rbrace =2I\end{aligned}}

اکیوئیشن دا 3-ایامی ورژن اسطراں حاصل ہندا اے؛

{\begin{aligned}-i\gamma _{i}\partial _{i}\psi =(i\eta \partial _{t}+\eta ^{\dagger }m)\psi \end{aligned}}

اتھے

$\eta =(\gamma _{0}+i\gamma _{5})/{\sqrt {2}}$ اک $4\times 4$ نلپوٹینٹ میٹرکس ہندا اے, اتے
$\gamma _{i}$ ڈیراک گاما میٹرکس ( $i=1,2,3$ ) ہندے ہن۔

3 D اندر شروڈنگر اکیوئیشن نوں اپروکت اکیوئیشن نوں سکئیئر (طبقہ) کرکے حاصل کیتا جا سکدا اے۔

غیر-ساپیکھک (نون-ریلیٹیوسٹک) حد $E-m\simeq E'$ اتے $E+m\simeq 2m$ وچ, اوپروکت اکیوئیشن نوں ڈیراک اکیوئیشن توں ویونتبدّ کیتا جا سکدا اے۔^[۴۲]

ایہہ وی دیکھو

نوٹس

↑ "Physicist Erwin Schrdinger's Google doodle marks quantum mechanics work". The Guardian. 13 اگست 2013. https://www.theguardian.com/technology/2013/aug/12/erwin-schrodinger-google-doodle. Retrieved on
25 اگست 2013.
↑ ^۲.۰ ^۲.۱ Schrdinger, E. (1926). "An Undulatory Theory of the Mechanics of Atoms and Molecules". Physical Review 28 (6): 1049–1070. doi:10.1103/PhysRev.28.1049. Bibcode: 1926PhRv.۔.28.1049S. http://home.tiscali.nl/physis/HistoricPaper/Schroedinger/Schroedinger1926c.pdf.
↑ Lua error in package.lua at line 80: module 'Module:Citation/CS1/COinS' not found.
↑ Lua error in package.lua at line 80: module 'Module:Citation/CS1/COinS' not found.
↑ ^۵.۰ ^۵.۱ ^۵.۲ ^۵.۳ ^۵.۴ Shankar, R. (1994). Principles of Quantum Mechanics, 2nd, Kluwer Academic/Plenum Publishers. ISBN 978-0-306-44790-7.
↑ "Schrodinger equation"۔ hyperphysics.phy-astr.gsu.edu۔
↑ (1995) Modern Quantum Mechanics. Reading, Massachusetts: Addison-Wesley, 68.
↑ Nouredine Zettili (17 فروری 2009). Quantum Mechanics: Concepts and Applications. John Wiley & Sons. ISBN 978-0-470-02678-6.
↑ Lua error in package.lua at line 80: module 'Module:Citation/CS1/COinS' not found.
↑ David Deutsch, The Beginning of infinity, page 310
↑ de Broglie, L. (1925). "Recherches sur la thorie des quanta". Annales de Physique 10 (3): 22–128. http://tel.archives-ouvertes.fr/docs/00/04/70/78/PDF/tel-00006807.pdf. Translated version at the وے بیک مشین (archived 9 مئی 2009)۔
↑ Weissman, M.B.; V. V. Iliev; I. Gutman (2008). "A pioneer remembered: biographical notes about Arthur Constant Lunn". Communications in Mathematical and in Computer Chemistry 59 (3): 687–708.
↑ Kamen, Martin D. (1985). Radiant Science, Dark Politics. Berkeley and Los Angeles, CA: University of California Press, 29–32. ISBN 0-520-04929-2.
↑ Schrodinger, E. (1984). Collected papers. Friedrich Vieweg und Sohn. ISBN 3-7001-0573-8. See introduction to first 1926 paper.
↑ ^۱۵.۰ ^۱۵.۱ Encyclopaedia of Physics (2nd Edition), R.G. Lerner, G.L. Trigg, VHC publishers, 1991, (Verlagsgesellschaft) 3-527-26954-1, (VHC Inc.) سانچہ:Isbn
↑ Sommerfeld, A. (1919). Atombau und Spektrallinien. Braunschweig: Friedrich Vieweg und Sohn. ISBN 3-87144-484-7.
↑ For an English source, see Haar, T.. The Old Quantum Theory.
↑ Rhodes, R. (1986). Making of the Atomic Bomb. Touchstone. ISBN 0-671-44133-7.
↑ ^۱۹.۰ ^۱۹.۱ Erwin Schrdinger (1982). Collected Papers on Wave Mechanics: Third Edition. American Mathematical Soc.. ISBN 978-0-8218-3524-1.
↑ Schrdinger, E. (1926). "Quantisierung als Eigenwertproblem؛ von Erwin Schrdinger". Annalen der Physik 384: 361–377. doi:10.1002/andp.19263840404. Bibcode: 1926AnP.۔.384.۔361S. http://gallica.bnf.fr/ark:/12148/bpt6k153811.image.langFR.f373.pagination.
↑ Erwin Schrdinger, "The Present situation in Quantum Mechanics," p. 9 of 22. The English version was translated by John D. Trimmer. The translation first appeared first in Proceedings of the American Philosophical Society, 124, 323–38. It later appeared as Section I.11 of Part I of Quantum Theory and Measurement by J.A. Wheeler and W.H. Zurek, eds., Princeton University Press, New Jersey 1983.
↑ Einstein, A.; et. al۔. Letters on Wave Mechanics: Schrodinger–Planck–Einstein–Lorentz.
↑ ^۲۳.۰ ^۲۳.۱ ^۲۳.۲ Moore, W.J. (1992). Schrdinger: Life and Thought. Cambridge University Press. ISBN 0-521-43767-9.
↑ It is clear that even in his last year of life, as shown in a letter to Max Born, that Schrdinger never accepted the Copenhagen interpretation.^[۲۳]^:220
↑ Takahisa Okino (2013). "Correlation between Diffusion Equation and Schrdinger Equation". Journal of Modern Physics (4): 612–615. https://dx.doi.org/10.4236/jmp.2013.45088.
↑ ^۲۶.۰ ^۲۶.۱ Molecular Quantum Mechanics Parts I and II: An Introduction to Quantum Chemistry (Volume 1), P.W. Atkins, Oxford University Press, 1977, سانچہ:Isbn
↑ دی نیو کوانٹم یونیورس, T.Hey, P.Walters, Cambridge University Press, 2009, سانچہ:Isbn
↑ ^۲۸.۰ ^۲۸.۱ ^۲۸.۲ ^۲۸.۳ Quanta: A handbook of concepts, P.W. Atkins, Oxford University Press, 1974, سانچہ:Isbn
↑ ^۲۹.۰ ^۲۹.۱ Physics of Atoms and Molecules, B.H. Bransden, C.J.Joachain, Longman, 1983, سانچہ:Isbn
↑ ^۳۰.۰ ^۳۰.۱ Quantum Physics of Atoms, Molecules, Solids, Nuclei and Particles (2nd Edition), R. Resnick, R. Eisberg, John Wiley & Sons, 1985, سانچہ:Isbn
↑ ^۳۱.۰ ^۳۱.۱ ^۳۱.۲ Quantum Mechanics Demystified, D. McMahon, Mc Graw Hill (USA), 2006, سانچہ:Isbn
↑ ^۳۲.۰ ^۳۲.۱ Analytical Mechanics, L.N. Hand, J.D. Finch, Cambridge University Press, 2008, سانچہ:Isbn
↑ N. Zettili. Quantum Mechanics: Concepts and Applications, 2nd, 458. ISBN 978-0-470-02679-3.
↑ Physical chemistry, P.W. Atkins, Oxford University Press, 1978, سانچہ:Isbn
↑ Solid State Physics (2nd Edition), J.R. Hook, H.E. Hall, Manchester Physics Series, John Wiley & Sons, 2010, سانچہ:Isbn
↑ Physics for Scientists and Engineers – with Modern Physics (6th Edition), P. A. Tipler, G. Mosca, Freeman, 2008, سانچہ:Isbn
↑ David Griffiths (2008). Introduction to elementary particles. Wiley-VCH, 162–. ISBN 978-3-527-40601-2. Retrieved on 27 جون 2011.
↑ ^۳۸.۰ ^۳۸.۱ ^۳۸.۲ Quantum Mechanics, E. Abers, Pearson Ed., Addison Wesley, Prentice Hall Inc, 2004, سانچہ:Isbn
↑ http://www.stt.msu.edu/~mcubed/Relativistic.pdf
↑ Takahisa Okino (2015). "Mathematical Physics in Diffusion Problems". Journal of Modern Physics (6): 2109–2144. https://dx.doi.org/10.4236/jmp.2015.614217.
↑ Ajaib, Muhammad Adeel (2015). "A Fundamental Form of the Schrdinger Equation". Found.Phys. 45 (2015) no.12, 1586–1598. doi:10.1007/s10701-015-9944-z. Bibcode: 2015FoPh.۔.45.1586A. https://link.springer.com/article/10.1007٪2Fs10701-015-9944-z.
↑ ^۴۲.۰ ^۴۲.۱ Ajaib, Muhammad Adeel (2016). "Non-Relativistic Limit of the Dirac Equation". International Journal of Quantum Foundations. http://www.ijqf.org/archives/3574.
↑ Lvy-Leblond, J-۔M. (1967). "Nonrelativistic particles and wave equations". Comm. Math. Pays. 6 (4): 286–311. https://projecteuclid.org/euclid.cmp/1103840281.

حوالے

P. A. M. Dirac (1958). The Principles of Quantum Mechanics, 4th, Oxford University Press.
(2000) Quantum Mechanics, 2nd, Prentice Hall PTR. ISBN 0-582-35691-1.
David J. Griffiths (2004). Introduction to Quantum Mechanics, 2nd, Benjamin Cummings. ISBN 0-13-124405-1.
Richard Liboff (2002). Introductory Quantum Mechanics, 4th, Addison Wesley. ISBN 0-8053-8714-5.
David Halliday (2007). Fundamentals of Physics, 8th, Wiley. ISBN 0-471-15950-6.
Serway, Moses, and Moyer (2004). Modern Physics, 3rd, Brooks Cole. ISBN 0-534-49340-8.
Schrdinger, Erwin (دسمبر 1926). "An Undulatory Theory of the Mechanics of Atoms and Molecules". Phys. Rev. 28 (6): 1049–1070. doi:10.1103/PhysRev.28.1049. Bibcode: 1926PhRv.۔.28.1049S.
Teschl (2009). Mathematical Methods in Quantum Mechanics؛ With Applications to Schrdinger Operators. American Mathematical Society. ISBN 978-0-8218-4660-5.

باہری لنک

Lua error in package.lua at line 80: module 'Module:Citation/CS1/COinS' not found.
Quantum Physics Archived 2012-03-07 at the وے بیک مشین – textbook by Benjamin Crowell with a treatment of the time-independent Schrdinger equation
Linear Schrdinger Equation at EqWorld: The World of Mathematical Equations.
Nonlinear Schrdinger Equation at EqWorld: The World of Mathematical Equations.
The Schrdinger Equation in One Dimension as well as the directory of the book۔
All about 3D Schrdinger Equation
Mathematical aspects of Schrdinger equations are discussed on the Dispersive PDE Wiki Archived 2017-07-23 at the وے بیک مشین۔
Web-Schrdinger: Interactive solution of the 2D time-dependent and stationary Schrdinger equation
An alternate reasoning behind the Schrdinger Equation
Online software-Periodic Potential Lab Solves the time-independent Schrdinger equation for arbitrary periodic potentials.
What Do You Do With a Wavefunction؟
The Young Double-Slit Experiment

سانچہ:کوانٹم مکینکس ٹوپک

[1] "Physicist Erwin Schrdinger's Google doodle marks quantum mechanics work". The Guardian. 13 اگست 2013. https://www.theguardian.com/technology/2013/aug/12/erwin-schrodinger-google-doodle. Retrieved on
25 اگست 2013.

[sch-2] ۲.۰ ^۲.۱ Schrdinger, E. (1926). "An Undulatory Theory of the Mechanics of Atoms and Molecules". Physical Review 28 (6): 1049–1070. doi:10.1103/PhysRev.28.1049. Bibcode: 1926PhRv.۔.28.1049S. http://home.tiscali.nl/physis/HistoricPaper/Schroedinger/Schroedinger1926c.pdf.

[Griffiths2004-3] Lua error in package.lua at line 80: module 'Module:Citation/CS1/COinS' not found.

[Laloe-4] Lua error in package.lua at line 80: module 'Module:Citation/CS1/COinS' not found.

[Shankar1994-5] ۵.۰ ^۵.۱ ^۵.۲ ^۵.۳ ^۵.۴ Shankar, R. (1994). Principles of Quantum Mechanics, 2nd, Kluwer Academic/Plenum Publishers. ISBN 978-0-306-44790-7.

[6] "Schrodinger equation"۔ hyperphysics.phy-astr.gsu.edu۔

[7] (1995) Modern Quantum Mechanics. Reading, Massachusetts: Addison-Wesley, 68.

[Zettili2009-8] Nouredine Zettili (17 فروری 2009). Quantum Mechanics: Concepts and Applications. John Wiley & Sons. ISBN 978-0-470-02678-6.

[Ballentine-9] Lua error in package.lua at line 80: module 'Module:Citation/CS1/COinS' not found.

[10] David Deutsch, The Beginning of infinity, page 310

[11] Broglie, L. (1925). "Recherches sur la thorie des quanta". Annales de Physique 10 (3): 22–128. http://tel.archives-ouvertes.fr/docs/00/04/70/78/PDF/tel-00006807.pdf. Translated version at the وے بیک مشین (archived 9 مئی 2009)۔

[12] Weissman, M.B.; V. V. Iliev; I. Gutman (2008). "A pioneer remembered: biographical notes about Arthur Constant Lunn". Communications in Mathematical and in Computer Chemistry 59 (3): 687–708.

[13] Kamen, Martin D. (1985). Radiant Science, Dark Politics. Berkeley and Los Angeles, CA: University of California Press, 29–32. ISBN 0-520-04929-2.

[14] Schrodinger, E. (1984). Collected papers. Friedrich Vieweg und Sohn. ISBN 3-7001-0573-8. See introduction to first 1926 paper.

[verlagsgesellschaft1991-15] ۱۵.۰ ^۱۵.۱ Encyclopaedia of Physics (2nd Edition), R.G. Lerner, G.L. Trigg, VHC publishers, 1991, (Verlagsgesellschaft) 3-527-26954-1, (VHC Inc.) سانچہ:Isbn

[16] Sommerfeld, A. (1919). Atombau und Spektrallinien. Braunschweig: Friedrich Vieweg und Sohn. ISBN 3-87144-484-7.

[17] For an English source, see Haar, T.. The Old Quantum Theory.

[18] Rhodes, R. (1986). Making of the Atomic Bomb. Touchstone. ISBN 0-671-44133-7.

[Schrdinger1982-19] ۱۹.۰ ^۱۹.۱ Erwin Schrdinger (1982). Collected Papers on Wave Mechanics: Third Edition. American Mathematical Soc.. ISBN 978-0-8218-3524-1.

[20] Schrdinger, E. (1926). "Quantisierung als Eigenwertproblem؛ von Erwin Schrdinger". Annalen der Physik 384: 361–377. doi:10.1002/andp.19263840404. Bibcode: 1926AnP.۔.384.۔361S. http://gallica.bnf.fr/ark:/12148/bpt6k153811.image.langFR.f373.pagination.

[21] Erwin Schrdinger, "The Present situation in Quantum Mechanics," p. 9 of 22. The English version was translated by John D. Trimmer. The translation first appeared first in Proceedings of the American Philosophical Society, 124, 323–38. It later appeared as Section I.11 of Part I of Quantum Theory and Measurement by J.A. Wheeler and W.H. Zurek, eds., Princeton University Press, New Jersey 1983.

[22] Einstein, A.; et. al۔. Letters on Wave Mechanics: Schrodinger–Planck–Einstein–Lorentz.

[Moore1992-23] ۲۳.۰ ^۲۳.۱ ^۲۳.۲ Moore, W.J. (1992). Schrdinger: Life and Thought. Cambridge University Press. ISBN 0-521-43767-9.

[24] It is clear that even in his last year of life, as shown in a letter to Max Born, that Schrdinger never accepted the Copenhagen interpretation.^[۲۳]^:220

[25] Takahisa Okino (2013). "Correlation between Diffusion Equation and Schrdinger Equation". Journal of Modern Physics (4): 612–615. https://dx.doi.org/10.4236/jmp.2013.45088.

[Quantum_Chemistry_1977-26] ۲۶.۰ ^۲۶.۱ Molecular Quantum Mechanics Parts I and II: An Introduction to Quantum Chemistry (Volume 1), P.W. Atkins, Oxford University Press, 1977, سانچہ:Isbn

[27] دی نیو کوانٹم یونیورس, T.Hey, P.Walters, Cambridge University Press, 2009, سانچہ:Isbn

[Quanta_1974-28] ۲۸.۰ ^۲۸.۱ ^۲۸.۲ ^۲۸.۳ Quanta: A handbook of concepts, P.W. Atkins, Oxford University Press, 1974, سانچہ:Isbn

[Molecules,_B.H._Bransden_1983-29] ۲۹.۰ ^۲۹.۱ Physics of Atoms and Molecules, B.H. Bransden, C.J.Joachain, Longman, 1983, سانچہ:Isbn

[Atoms,_Molecules_1985-30] ۳۰.۰ ^۳۰.۱ Quantum Physics of Atoms, Molecules, Solids, Nuclei and Particles (2nd Edition), R. Resnick, R. Eisberg, John Wiley & Sons, 1985, سانچہ:Isbn

[Quantum_Mechanics_Demystified_2006-31] ۳۱.۰ ^۳۱.۱ ^۳۱.۲ Quantum Mechanics Demystified, D. McMahon, Mc Graw Hill (USA), 2006, سانچہ:Isbn

[Analytical_Mechanics_2008-32] ۳۲.۰ ^۳۲.۱ Analytical Mechanics, L.N. Hand, J.D. Finch, Cambridge University Press, 2008, سانچہ:Isbn

[33] N. Zettili. Quantum Mechanics: Concepts and Applications, 2nd, 458. ISBN 978-0-470-02679-3.

[34] Physical chemistry, P.W. Atkins, Oxford University Press, 1978, سانچہ:Isbn

[35] Solid State Physics (2nd Edition), J.R. Hook, H.E. Hall, Manchester Physics Series, John Wiley & Sons, 2010, سانچہ:Isbn

[36] Physics for Scientists and Engineers – with Modern Physics (6th Edition), P. A. Tipler, G. Mosca, Freeman, 2008, سانچہ:Isbn

[37] David Griffiths (2008). Introduction to elementary particles. Wiley-VCH, 162–. ISBN 978-3-527-40601-2. Retrieved on 27 جون 2011.

[Quantum_Mechanics_2004-38] ۳۸.۰ ^۳۸.۱ ^۳۸.۲ Quantum Mechanics, E. Abers, Pearson Ed., Addison Wesley, Prentice Hall Inc, 2004, سانچہ:Isbn

[39] ttp://www.stt.msu.edu/~mcubed/Relativistic.pdf

[40] Takahisa Okino (2015). "Mathematical Physics in Diffusion Problems". Journal of Modern Physics (6): 2109–2144. https://dx.doi.org/10.4236/jmp.2015.614217.

[one-41] Ajaib, Muhammad Adeel (2015). "A Fundamental Form of the Schrdinger Equation". Found.Phys. 45 (2015) no.12, 1586–1598. doi:10.1007/s10701-015-9944-z. Bibcode: 2015FoPh.۔.45.1586A. https://link.springer.com/article/10.1007٪2Fs10701-015-9944-z.

[two-42] ۴۲.۰ ^۴۲.۱ Ajaib, Muhammad Adeel (2016). "Non-Relativistic Limit of the Dirac Equation". International Journal of Quantum Foundations. http://www.ijqf.org/archives/3574.

[three-43] Lvy-Leblond, J-۔M. (1967). "Nonrelativistic particles and wave equations". Comm. Math. Pays. 6 (4): 286–311. https://projecteuclid.org/euclid.cmp/1103840281.

[۱]

[۲]

[۳]

[۴]

[۵]

[۶]

[۷]

[۸]

[۹]

[۱۰]

[۱۱]

[۱۲]

[۱۳]

[۱۴]

[۱۵]

[۱۶]

[۱۷]

[۱۸]

[۱۹]

[۲۰]

[۲۱]

[۲۲]

[۲۳]

[۲۴]

[۲۵]

[۲۶]

[۲۷]

[۲۸]

[۲۹]

[۳۰]

[۳۱]

[۳۲]

[۳۳]

[۳۴]

[۳۵]

[۳۶]

[۳۷]

[۳۸]

[۳۹]

[۴۰]

[۴۱]

[۴۲]

[۴۳]